经典论文阅读(五)--Factorization Machines(FM)

Factorization Machines(FM)

1. 摘要

FM综合了SVM和factorization models的优势。
FMs是一种适用于任何实值特征向量的通用预测器。与支持向量机相比，FMs使用因式分解的参数来建模变量之间的所有交互作用。因此，即使在支持向量机失效的情况下(比如推荐系统)，它们也能够估计交互作用(interactions)。
结果表明，FMs的模型方程可以在线性时间内计算，从而可以直接优化FMs。因此，与非线性SVM不同的是，不需要对偶形式的转换，可以直接估计模型参数，而不需要求解中任何支持向量。我们展示了它与支持向量机的关系，以及FMs在稀疏情况下参数估计中的优势。

我们还表明，FMs包含(subsume)了许多最成功的协同过滤方法，包括biased MF, SVD++, PITF 以及FPMC。
FM的优势：

1. FM允许在非常稀疏的数据上进行参数估计，而SVMS是失败的。
2. FMs具有线性复杂度，可以在原始条件下进行优化，不像支持向量机那样依赖支持向量。我们展示了FMs可以扩展到像Netflix这样拥有1亿个训练实例的大型数据集。
3. FMs是一种通用的预测器，可以用于任何实值特征向量。与此相反，其他state-of-the-art的因子分解模型只能在非常有限的输入数据上工作。我们将说明，通过定义输入数据的特征向量，FMs可以模拟其他state-of-the-art的模型，如偏置MF、SVD++、PITF或FPMC。

2. Factorization Machines(FM)

A. FM模型

定义度为2的二次因子机模型方程如下：
   $\hat{y}(\textbf{x}) := \omega_0 + \sum\limits_{i=1}^{n}\omega_i x_i + \sum\limits_{i=1}^{n}\sum\limits_{j=i+1}^{n} \left\langle \textbf{v}_i,\textbf{v}_j \right\rangle x_ix_j \qquad (1)$y^​(x):=ω0​+i=1∑n​ωi​xi​+i=1∑n​j=i+1∑n​⟨vi​,vj​⟩xi​xj​(1)
其中模型参数限制在 $\omega_0 \in \mathbb{R},\textbf{w}\in \mathbb{R}^n,\textbf{V}\in \mathbb{R}^{n\times k}$ω0​∈R,w∈Rn,V∈Rn×k
$\left\langle .,. \right\rangle$⟨.,.⟩ 是两个大小为k的向量的点乘(内积)：
     $\left\langle \textbf{v}_i,\textbf{v}_j \right\rangle := \sum\limits_{f=1}^{k}v_{i,f}\cdot v_{j,f}$⟨vi​,vj​⟩:=f=1∑k​vi,f​⋅vj,f​
行向量$v_i$vi​表示有k个因子的第i个变量，k 是个超参数，它定义了因式分解的维度。
< $v_i,v_j$vi​,vj​ > 内积后的矩阵$V=(v_1,v_2,...,v_n)$V=(v1​,v2​,...,vn​)是一个$k\times n$k×n的矩阵，k << n。

二次的FM捕获了变量之间所有单个的和成对(pairwise)的interactions:

• $\omega_0$ω0​ 是全局的偏差bias；
• $\omega_i$ωi​ 对第i个变量的强度建模；
• $\hat{\omega}_{i,j} := \left\langle \textbf{v}_i,\textbf{v}_j \right\rangle$ω^i,j​:=⟨vi​,vj​⟩ 对第i和第j个变量之间的交互作用建模。对于每个交互作用，FM不是使用每个interaction自己的参数$\omega_{i,j}$ωi,j​，而是通过因子分解对交互作用进行建模。这是稀疏环境下允许高阶交互的高质量参数估计的关键the key point。

由于矩阵分解$W=V\cdot V^t$W=V⋅Vt，只要k足够大，FM就可以表达任意交互矩阵W。然而在稀疏的设置下，通常应该选用一个较小的k，因为没有足够的数据来估计复杂的交互作用。而且限制k比较小，可以获得较好的泛化性能。

B. 计算复杂度

FM方程中由于交叉项的存在：$\sum\limits_{i=1}^{n}\sum\limits_{j=i+1}^{n} \left\langle \textbf{v}_i,\textbf{v}_j \right\rangle x_ix_j$i=1∑n​j=i+1∑n​⟨vi​,vj​⟩xi​xj​，直接计算的时间复杂度是$k \large O(n^2)$kO(n2)。因为两层循环$\large O(n^2)$O(n2)，循环内部又有k维的内积$\large O(k)$O(k)。交叉项化简后，复杂度可以降到 $\large O(kn)$O(kn)。
推导如下：

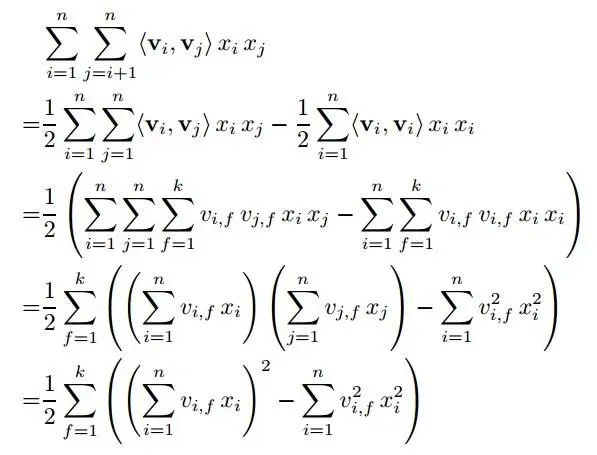
而且，稀疏情况下大部分X元素值为0，所以外层的sum加和只需要对非零的元素来计算。

C. 梯度学习

模型参数可以用随机梯度下降(SGD)的方法学习出来。FM的梯度如下：

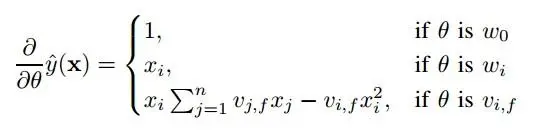
通常，每个梯度可以在常数时间内计算出来。稀疏情况下，所有参数的更新可以在$\large O(kn)$O(kn)的时间内得出。

FMs使用分解的交互作用而不是完全参数化的交互作用，来对特征向量x中所有可能的交互作用进行建模。
这有两个主要优点:
1）即使在高度稀疏的情况下，也可以估计特征之间的相互作用。特别是，它有可能推广到未观察到的相互作用。
2）参数的数量以及预测和学习的时间是线性的。这使得使用SGD直接优化可行，并允许针对各种损失函数进行优化(比如平方损失，对数损失甚至Hinge loss)。

3. FM与SVM

svm使用线性核时，$K_l(\bf{x},\bf{z}):= 1+\left\langle\bf{x},\bf{z}\right\rangle$Kl​(x,z):=1+⟨x,z⟩，相当于映射了
$\phi(\bf{x}):=(1,x_1,x_2,...x_n)$ϕ(x):=(1,x1​,x2​,...xn​)，那么模型的方程可以写成：
     $\hat{y}(\bf{x})=\omega_0 + \sum\limits_{i=1}^{n}\omega_i x_i$y^​(x)=ω0​+i=1∑n​ωi​xi​

很明显线性SVM是FM在一阶时的特殊情况。

多项式核

多项式核使得SVM可以对变量之间的高阶交互作用建模。核函数 $K(x,z):=(\left\langle x,z \right\rangle + 1)^d$K(x,z):=(⟨x,z⟩+1)d
对应二阶的映射函数：
$\phi(x):=(1,\sqrt{2}x_1,...,\sqrt{2}x_n,\, x_1^2,...,x_n^2, \\ \sqrt{2}x_1x_2,...\sqrt{2}x_1x_n,\,\, \sqrt{2}x_2x_3,...,\sqrt{2}x_{n-1}x_n)$ϕ(x):=(1,2​x1​,...,2​xn​,x12​,...,xn2​,2​x1​x2​,...2​x1​xn​,2​x2​x3​,...,2​xn−1​xn​)
注：实践中SVM使用映射函数的对偶形式优化求解。

因此，多项式支持向量机的模型方程可以改写为
$\hat{y}(\bf{x})=\omega_0 + \sqrt{2}\sum\limits_{i=1}^{n}\omega_i x_i + \sum\limits_{i=1}^{n}\omega_{i,i}^{(2)}x_i^2 + \sqrt{2}\sum\limits_{i=1}^{n}\sum\limits_{j=i+1}^{n}\omega_{i,i}^{(2)}x_ix_j$y^​(x)=ω0​+2​i=1∑n​ωi​xi​+i=1∑n​ωi,i(2)​xi2​+2​i=1∑n​j=i+1∑n​ωi,i(2)​xi​xj​

可以看到，这两种方法都对所有嵌套的交互进行了建模(二阶 degree=2).
SVM与FMs的主要区别在于参数：
支持向量机的所有交互参数$\omega_{i,j}$ωi,j​都是完全独立的，例如$\omega_{i,j}$ωi,j​和$\omega_{i,l}$ωi,l​。
与此相反，FMs的交互参数被分解，$\left\langle \bf{v}_i,\bf{v}_j \right\rangle$⟨vi​,vj​⟩和$\left\langle \bf{v}_i,\bf{v}_l \right\rangle$⟨vi​,vl​⟩由于参数的重叠和共享而相互依赖。

这也是多项式核SVM在高稀疏环境下不能学习到交叉项模型的原因：因为 $\omega_{ij}$ωij​与$\omega_{il}$ωil​彼此独立，要学习参数$\omega_{ij}$ωij​，必须保证特征 i 与特征 j 同时不为0，这在协同过滤以及高稀疏环境下是难以保证的。

4. 结论

在本文中，我们引入了因子分解机。FMs结合了支持向量机的一般性和因子分解模型的优点。与支持向量机相比，(1)FMs能够在极大稀疏性下估计参数，(2)模型方程是线性的，仅依赖于模型参数，因此它们可以直接在原始状态下进行优化。

FMs的表达能力与多项式支持向量机的表达能力是相似的。与像PARAFAC这样的张量因子分解模型相比，FMs是一个可以处理任何实值向量的通用预测器。此外，只要在输入特征向量中使用正确的indicators，FMs就与许多仅适用于特定任务的state-of-the-art的模型完全相同或非常相似，其中有偏置MF、SVD++、PITF和FPMC。