Boosting

Boosting策略在上一篇中有提到过，这里再说一遍。

Boosting策略的核心思想就是对错误分类的样本投入更大的关注。采用的是加法模型和向前分步算法，向前分步算法中的每一步都会改变样本的权重。

模型是加法模型、损失函数为指数函数、学习算法为前向分步算法的二类分类学习方法

一、AdaBoost简介

      Boosting, 也称为增强学习或提升法，是一种重要的集成学习技术， 能够将预测精度仅比随机猜度略高的弱学习器增强为预测精度高的强学习器，这在直接构造强学习器非常困难的情况下，为学习算法的设计提供了一种有效的新思路和新方法。其中最为成功应用的是，Yoav Freund和Robert Schapire在1995年提出的AdaBoost算法。
      AdaBoost是英文"Adaptive Boosting"（自适应增强）的缩写，它的自适应在于：前一个基本分类器被错误分类的样本的权值会增大，而正确分类的样本的权值会减小，并再次用来训练下一个基本分类器。同时，在每一轮迭代中，加入一个新的弱分类器，直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数才确定最终的强分类器。

弱分类器：

什么是弱分类器，只比随机猜测好一点点的分类器叫弱分类器。就比如一个强分类器来判断这是一只猫还是一只狗，它可能会给出，这张图片有0.99的概率为狗。那么弱分类器就只能够说这张图片有0.55的概率是狗。只比随机猜测要好一点点。

弱分类器的优势是什么？弱分类器的特性就是high-bias & low variance（高偏差-低方差），其与生俱来的优点就是泛化性能好。因此，将多个算法组合起来之后，可以达到降偏差的效果，进而得到一个偏差小、方差小的泛化能力好的模型。

所以说Boosting与bagging很大不同的一点就是，boosting是通过集成模型来降低偏差，而bagging是通过集成模型来降低方差。

常用的弱分类器像决策树桩，ID3，C4.5,CART因为决策树很容易过拟合，所以说用这些树模型的时候一定要预剪枝限制深度等或者后剪枝，总之要低方差，偏差高无所谓。

Adaboost算法流程：

1. 初始化强分类器，样本权重初始化为
2. 构建最小化误差的基分类器(决策树桩，ID3，C4.5，CART)
3. 计算错分率，计算表决系数
4. 更新权重（Z为归一化因子，其实就是所有的和）
5. 更新强分类器
6. 重复2-5步骤，直到错分率小于一定阈值或者迭代达到一定步数。
7. 得到最终的分类器，(sign符号函数，>0为1，<0为-1)

另一种符号表示的

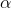的推导 训练误差界

最终得到的分类器是，如果，有，则，如果，有，则,那么有下式

                                                         (1)

简单说就是不想等的时候左边为1，右边>=1。想等的时候左边为0，右边>=0.

再根据权值的更新公式，变下型

有

接下来就可以开始正式的推导了。

（1）式右端项有

公式编辑器好蛋疼。直接上图吧，符号有一点不一样。

因此可以得出，Adaboost的误差界为

它的就是我这里的

权值更新也可以重新推导，不再需要去复杂的计算。缩放就可以得到下一步迭代的新的权重。

戏称为Thank God Hole

AdaBoost应到到多分类场景

1. 最简单的方法就是One Vs One 或者One Vs All
2. 或者也可以用softmax
3. 也有针对多分类的Adaboost模型如Adaboost M1,Adaboost M2,Adaboost MH,Adaboost MR

M1,M2:https://blog.****.net/tyh70537/article/details/76675098

掌握上面这些推导理论基本上算是稳了。接下来讲一下adaboost的优缺点和应用场景。

Adaboost的回归算法

Adaboost R2：

其实大体的思路与分类算法一样，就是一些系数的计算更新公式变了，多分类也是这样的。

二分类的一个实例

https://blog.****.net/hffhjh111/article/details/72348378

优缺点和应用场景

优点

1. 用于二分类或多分类的应用场景
2. 在Adaboost的框架下，可以使用各种回归分类模型来构建弱学习器，非常灵活。
3. 无脑化，简单，不会overfitting，不用调分类器
4. 泛化错误率低，精度高，可应用在大部分分类器上，无需调整参数 
5. 用于特征选择（feature selection)

缺点

1. AdaBoost迭代次数也就是弱分类器数目不太好设定，可以使用交叉验证来进行确定。
2. 数据不平衡导致分类精度下降。
3. 训练比较耗时，每次重新选择当前分类器最好切分点。
4. 对离群点敏感
5. 在Adaboost训练过程中，Adaboost会使得难于分类样本的权值呈指数增长，训练将会过于偏向这类困难的样本，导致Adaboost算法易受噪声干扰

 

 

参考：http://www.csuldw.com/2016/08/28/2016-08-28-adaboost-algorithm-theory/