引入线性模型 linear regression

以房价和房子大小的数据来引入线性模型，并且提出几个概念

• m:训练集数目

• (x,y）表示一个训练样本

• (x,y）表示一个训练样本

• $(x^i,y^i）$(xi,yi）表示第i个训练样本
  我们的训练思路为
  训练集=> 学习算法=> (x->h->y)
  其中h是一个引导x->y的函数，称为假设函数，hypothesis
  $h_{\theta}=\theta_0 +\theta_1x$hθ​=θ0​+θ1​x

• 注意我们研究线性是学习的基础，并且这里我们研究的属于单个变量，为单变量线性回归～

假设函数和代价函数

我们采用的为平房误差代价函数
$J(\theta_0,\theta_1)=\frac{1}{2m} \sum_{i=1}^m(h_{\theta}(x^i)-y^i)^2$J(θ0​,θ1​)=2m1​i=1∑m​(hθ​(xi)−yi)2

作图分析

• 简化h为$h=\theta_1x$h=θ1​x，$J$J函数可以直接表达为：
  
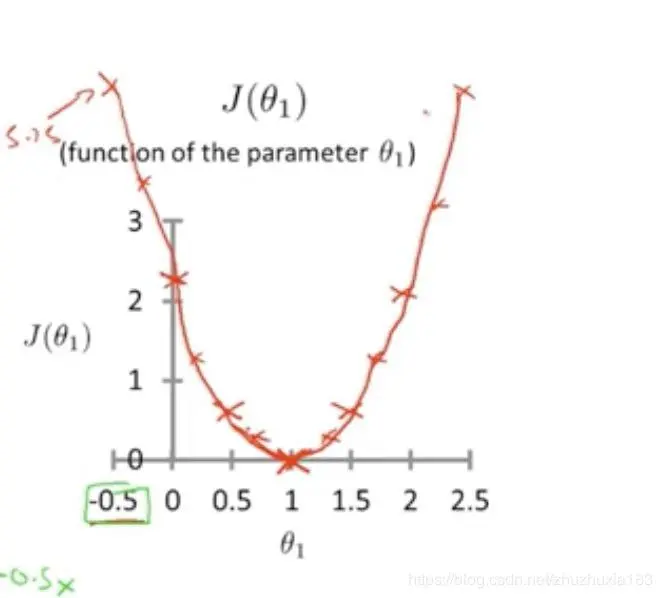
• 如果直接表达的话，三维模型如图
  
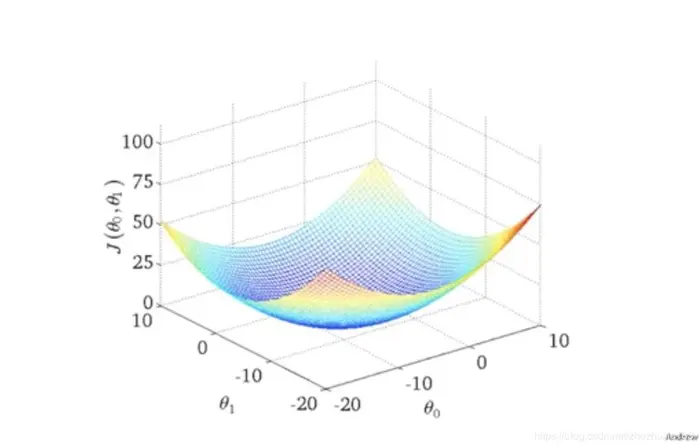
  采用等高线图为
  

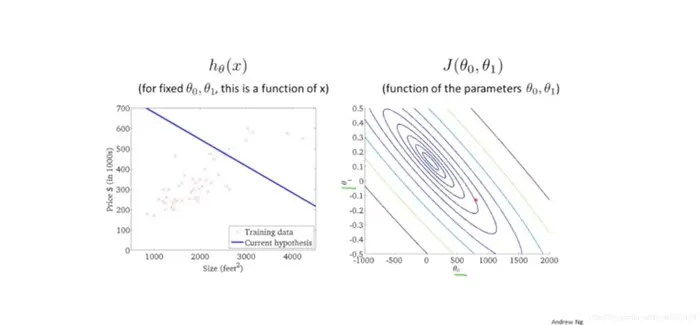
最小化的梯度下降法

通过最小化的梯度下降法来求解，步骤
1、给定$\theta_0,\theta_1$θ0​,θ1​初始值
2、$\theta_j=\theta_j-\alpha\frac{d(J(\theta_0,\theta_1))}{d\theta_j}$θj​=θj​−αdθj​d(J(θ0​,θ1​))​

• $\alpha$α我们称之为学习速率，太大太小都不好，如果太大，则会大致无法收敛甚至是发散的，太小会导致学习速率太小，收敛很慢
• $\frac{d(J_{\theta_0,\theta_1})}{d\theta_j}$dθj​d(Jθ0​,θ1​​)​我们称之为导数项，是求解下降的方向

注意是要同步更新，这才是梯度下降法的自然做法，不是串行

• 同时有不同的起始点，可能导致最终结果到不同的局部最小值
• 如果一开始就在局部最小值，$\theta$θ就不再变化，因为导数项为0
• 即使学习速率不变，梯度下降也是可以收敛到最小值的

梯度下降法+单变量线性回归

导数项为$\frac{d(J(\theta_0,\theta_1))}{d\theta_j}$dθj​d(J(θ0​,θ1​))​=>
$\frac{d\frac{1}{2m}\sum_{i=1}^m(\theta_0+\theta_1x^i-y^i)^2}{d\theta_j}$dθj​d2m1​∑i=1m​(θ0​+θ1​xi−yi)2​
=>
$\theta_0=\frac{1}{m} \sum_{i=1}^m(\theta_0+\theta_1x^i-y^i)$θ0​=m1​i=1∑m​(θ0​+θ1​xi−yi)

$\theta_1=\frac{1}{m} \sum_{i=1}^m(\theta_0+\theta_1x^i-y^i) x^i$θ1​=m1​i=1∑m​(θ0​+θ1​xi−yi)xi

• 我们采用的是同步更新，并且每次都是针对所有的数据进行梯度下降，遍历了整个训练集的样本，称之为Batch梯度下降
• Batch梯度下降，还有不需要遍历全部样本的梯度下降，遍历小子集