什么是反向传播（BP, Back Propagation）算法

$BP$BP算法（即误差反向传播算法）是适合于多层神经元网络的一种学习算法, 它建立在梯度下降法的基础上。$BP$BP网络的输入输出关系实质上是一种映射关系:一个$n$n输入$m$m输出的$BP$BP神经网络所完成的功能是从$n$n维欧氏空间向$m$m维欧氏空间中一有限域的连续映射,这一映射具有高度非线性。它的信息处理能力来源于简单非线性函数的多次复合, 因此具有很强的函数复现能力。这是$BP$BP算法得以应用的基础。

单个神经元的计算过程

如下图所示，

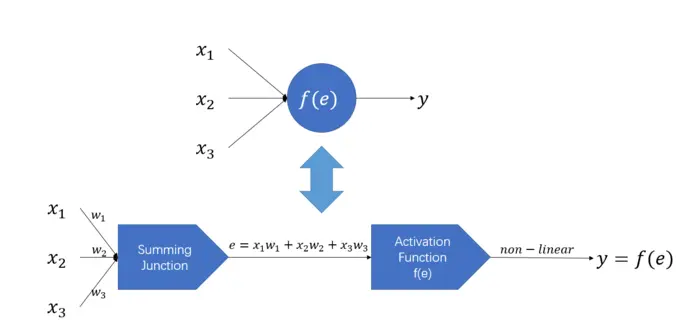
对于每个输入$x_i$xi​，分别乘以权重$w_i$wi​，求和，再经过一个非线性的**函数($sigmod$sigmod等)，得到输出$y$y
即
$y = f(e) \\ e = W^TX$y=f(e)e=WTX
$f(o)$f(o)是**函数，$W$W是权重矩阵（此处为行向量），$X$X为输入（行向量）。

反向传播算法计算过程

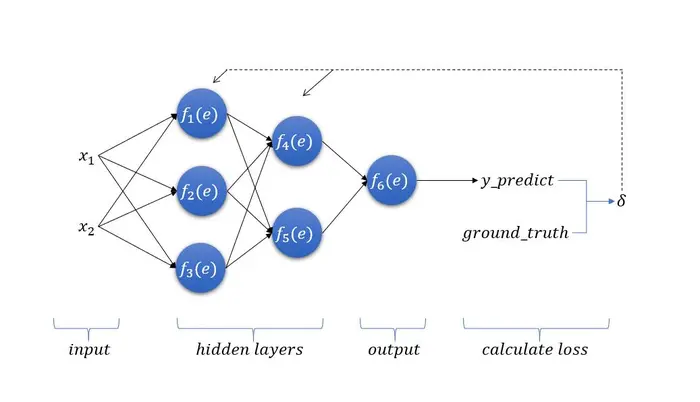
$BP$BP是一种反馈型学习网络，算法的学习过程包括两部分。
首先是信息的前向传播，然后是通过误差进行的反向传播。
通过神经网络的输入层将数据信息输入到神经网络，输入层的各个单元将数据传递给隐含层各个神经元进行。
反向传播算法的第一步是前向传播。

前向传播

$\left\{ \begin{aligned} y_1 & = & f_1(w_{(x_1)1}x_1+w_{(x_2)1}x_2)\\ y_2 & = & f_2(w_{(x_1)2}x_1+w_{(x_2)2}x_2)\\ y_3 & = & f_3(w_{(x_1)3}x_1+w_{(x_2)3}x_2)\\ y_4 & = & f_4(w_{14}y_1+w_{24}y_2+w_{34}y_3)\\ y_5 & = & f_5(w_{15}y_1+w_{25}y_2+w_{35}y_3)\\ y_6 & = & f_6(w_{46}y_4+w_{56}y_5)\\ y\_predict & = & y_6\\ \end{aligned} \right.$⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​y1​y2​y3​y4​y5​y6​y_predict​=======​f1​(w(x1​)1​x1​+w(x2​)1​x2​)f2​(w(x1​)2​x1​+w(x2​)2​x2​)f3​(w(x1​)3​x1​+w(x2​)3​x2​)f4​(w14​y1​+w24​y2​+w34​y3​)f5​(w15​y1​+w25​y2​+w35​y3​)f6​(w46​y4​+w56​y5​)y6​​
$w_{ij}$wij​表示第$i$i个节点对第$j$j个节点的权重。

计算代价$\delta$δ

一般情况下我们使用误差平方和表示代价。
即
$\delta=\frac{1}{2}(ground\_truth-y\_predict)^2$δ=21​(ground_truth−y_predict)2
当然极少数情况下我们也会使用简单的计算方式
$\delta = ground\_truth - y\_predict$δ=ground_truth−y_predict

反向传播

此时我们得到了最终的误差，也就是$f_6(e)$f6​(e)的误差$\delta$δ
反向传播给前面的神经元
$\delta_i$δi​表示第$i$i个神经元的误差。
$Second\_hidden\_layer\left\{ \begin{aligned} \delta_4 & = & w_{46}*\delta\\ \delta_5 & = & w_{56}*\delta\\ \end{aligned} \right.$Second_hidden_layer{δ4​δ5​​==​w46​∗δw56​∗δ​
下面计算第一个隐藏层
$First\_hidden\_layer\left\{ \begin{aligned} \delta_1 & = & w_{14}*\delta_4+w_{15}*\delta_5\\ \delta_2 & = & w_{24}*\delta_4+w_{25}*\delta_5\\ \delta_3 & = & w_{34}*\delta_4+w_{35}*\delta_5\\ \end{aligned} \right.$First_hidden_layer⎩⎪⎨⎪⎧​δ1​δ2​δ3​​===​w14​∗δ4​+w15​∗δ5​w24​∗δ4​+w25​∗δ5​w34​∗δ4​+w35​∗δ5​​

梯度下降法修正权重

$w'_{ij} = w_{ij} + bias_{ij}\\ bias_{ij} = \eta\delta_j\frac{\mathrm{d}f_j(e)}{\mathrm{d}e}element_i$wij′​=wij​+biasij​biasij​=ηδj​dedfj​(e)​elementi​
即
$w'_{ij} = w_{ij} + \eta\delta_j\frac{\mathrm{d}f_j(e)}{\mathrm{d}e}element_i$wij′​=wij​+ηδj​dedfj​(e)​elementi​
$w'_{ij}$wij′​是修正后的权重，$\eta$η是学习率，$e$e是**函数前的计算结果（本质就是对上一层结果的线性组合），$\frac{\mathrm{d}f_j(e)}{\mathrm{d}e}$dedfj​(e)​是这个神经元本身的结果对**函数前结果的导数，$\delta_i$δi​是第$i$i个神经元的代价，$element_i$elementi​就是元素i（也就是前面的那一个元素）。
为便于理解我们写一下式子，还是以下图这个为例。

$First\_hidden\_layer\left\{ \begin{aligned} w'_{x_11}=w_{x_11}+\eta\delta_1\frac{\mathrm{d}f_1(e)}{\mathrm{d}e}x_1\\ w'_{x_12}=w_{x_12}+\eta\delta_2\frac{\mathrm{d}f_2(e)}{\mathrm{d}e}x_1\\ w'_{x_13}=w_{x_13}+\eta\delta_3\frac{\mathrm{d}f_3(e)}{\mathrm{d}e}x_1\\ w'_{x_21}=w_{x_21}+\eta\delta_1\frac{\mathrm{d}f_1(e)}{\mathrm{d}e}x_2\\ w'_{x_22}=w_{x_11}+\eta\delta_2\frac{\mathrm{d}f_2(e)}{\mathrm{d}e}x_2\\ w'_{x_23}=w_{x_11}+\eta\delta_3\frac{\mathrm{d}f_3(e)}{\mathrm{d}e}x_2\\ \end{aligned} \right.$First_hidden_layer⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​wx1​1′​=wx1​1​+ηδ1​dedf1​(e)​x1​wx1​2′​=wx1​2​+ηδ2​dedf2​(e)​x1​wx1​3′​=wx1​3​+ηδ3​dedf3​(e)​x1​wx2​1′​=wx2​1​+ηδ1​dedf1​(e)​x2​wx2​2′​=wx1​1​+ηδ2​dedf2​(e)​x2​wx2​3′​=wx1​1​+ηδ3​dedf3​(e)​x2​​
$Second\_hidden\_layer\left\{ \begin{aligned} w'_{14}=w_{14}+\eta\delta_4\frac{\mathrm{d}f_4(e)}{\mathrm{d}e}y_1\\ w'_{24}=w_{14}+\eta\delta_4\frac{\mathrm{d}f_4(e)}{\mathrm{d}e}y_2\\ w'_{34}=w_{14}+\eta\delta_4\frac{\mathrm{d}f_4(e)}{\mathrm{d}e}y_3\\ w'_{15}=w_{15}+\eta\delta_4\frac{\mathrm{d}f_5(e)}{\mathrm{d}e}y_1\\ w'_{25}=w_{25}+\eta\delta_4\frac{\mathrm{d}f_5(e)}{\mathrm{d}e}y_2\\ w'_{35}=w_{35}+\eta\delta_4\frac{\mathrm{d}f_5(e)}{\mathrm{d}e}y_3\\ \end{aligned} \right.$Second_hidden_layer⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​w14′​=w14​+ηδ4​dedf4​(e)​y1​w24′​=w14​+ηδ4​dedf4​(e)​y2​w34′​=w14​+ηδ4​dedf4​(e)​y3​w15′​=w15​+ηδ4​dedf5​(e)​y1​w25′​=w25​+ηδ4​dedf5​(e)​y2​w35′​=w35​+ηδ4​dedf5​(e)​y3​​
$Output\_layer\left\{ \begin{aligned} w'_{46}=w_{46}+\eta\delta\frac{\mathrm{d}f_6(e)}{\mathrm{d}e}y_4\\ w'_{56}=w_{56}+\eta\delta\frac{\mathrm{d}f_6(e)}{\mathrm{d}e}y_5\\ \end{aligned} \right.$Output_layer⎩⎪⎪⎨⎪⎪⎧​w46′​=w46​+ηδdedf6​(e)​y4​w56′​=w56​+ηδdedf6​(e)​y5​​
这样我们就完成了一次每一层连接权值的修正。
接下来是下一轮的循环：利用修正完的模型，再输入一个样本，正向传播等到$y$y，再求$\delta$δ，再反向传播回来逐层修复权值。如此循环反复就是$BP$BP神经网络的计算原理了。

归一化

归一化方法

可见参考文献4的文章

• $min-max$min−max归一化：$x' = \frac{x-min}{max-min}$x′=max−minx−min​ 实现对原始数据的等比例缩放 [0-1]
• $zero-score$zero−score归一化：$x = \frac{x-\mu}{\delta}$x=δx−μ​ 期望为0，方差为1
• $y = 2*\frac{x - min }{max - min}-1$y=2∗max−minx−min​−1 最终数据区间[-1,1]

归一化作用

• 输入数据的单位不一样，有些数据的范围可能特别大，导致的结果是神经网络收敛慢、训练时间长。
• 数据范围大的输入在模式分类中的作用可能会偏大，而数据范围小的输入作用就可能会偏小。
• 由于神经网络输出层的**函数的值域是有限制的，因此需要将网络训练的目标数据映射到**函数的值域。例如神经网络的输出层若采用$S$S形** 函数，由于$S$S形函数的值域限制在$(0,1)$(0,1)，也就是说神经网络的输出只能限制在$(0,1)$(0,1)，所以训练数据的输出就要归一化到[0,1]区间。
• $S$S形**函数在$(0,1)$(0,1)区间以外区域很平缓，区分度太小。例如$S$S形函数$f(x)$f(x)在参数$a=1$a=1时，$f(100)$f(100)与$f(5)$f(5)只相差$0.0067$0.0067。这样数据的差异就会失去意义！

各类函数

• 线性函数 $f(x) = k*x+c$f(x)=k∗x+c
• 斜坡函数
  $f(x)=\left\{ \begin{aligned} T, x>c\\ k*x, |x|\leq c\\ -T, x<-c\\ \end{aligned} \right.$f(x)=⎩⎪⎨⎪⎧​T,x>ck∗x,∣x∣≤c−T,x<−c​
• 阈值函数
  $f(x)=\left\{ \begin{aligned} 1, x\geq c\\ 0, x<c\\ \end{aligned} \right.$f(x)={1,x≥c0,x<c​
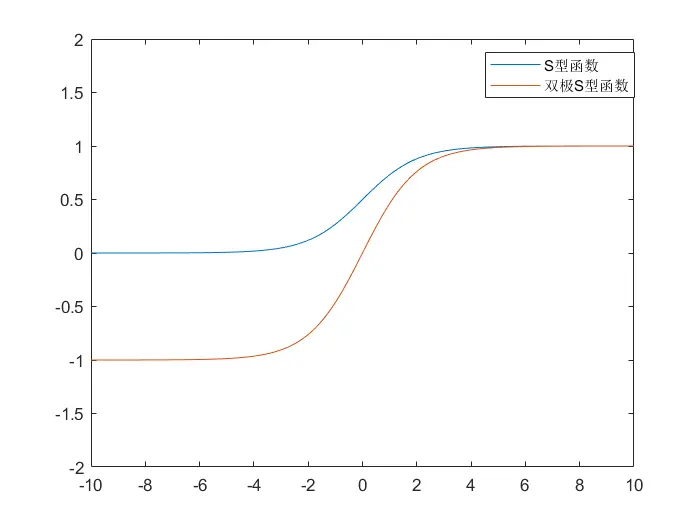
• $S$S型函数（$Sigmoid$Sigmoid）
  $f(x)=\frac{1}{1+e^{-\alpha x}} (0<f(x)<1)$f(x)=1+e−αx1​(0<f(x)<1)
  $f'(x) = \frac{\alpha e^{-\alpha x}}{(1+e^{-\alpha x})^2}=\alpha f(x)[1-f(x)]$f′(x)=(1+e−αx)2αe−αx​=αf(x)[1−f(x)]
• 双极$S$S型函数
  $f(x)=\frac{2}{1+e^{-\alpha x}}-1，(-1<f(x)<1)$f(x)=1+e−αx2​−1，(−1<f(x)<1)
  $f'(x)=\frac{2\alpha e^{-\alpha x}}{(1+e^{-\alpha x})^2}=\frac{\alpha [1-f(x)^2]}{2}$f′(x)=(1+e−αx)22αe−αx​=2α[1−f(x)2]​

参考文献

1王忠勇,陈恩庆,葛强,等.误差反向传播算法与信噪分离[J].河南科学,2002,01:7-10.

2许朋.基于BP神经网络的手写数字识别[J].科技视界,2020(11):51-53.

3奔跑的Yancy.BP神经网络：计算原理详解和MATLAB实现[EB/OL].https://blog.****.net/lyxleft/article/details/82840787 ,2018-09-25.

4刘林龙.2.7 理论 神经网络讲解[EB/OL].http://www.liulinlong.cn/index.php/archives/137/ ,2020-03-28.

[5]边华清.BP神经网络[EB/OL].https://blog.****.net/xiaobian_/article/details/105444399 ,2020-04-11.