Coursea-吴恩达-machine learning学习笔记（八）【week 4之Neural Networks: Representation】

神经网络(非线性分类)
产生的原因：尝试设计模仿大脑的算法。

神经元表示一个逻辑运算单元。
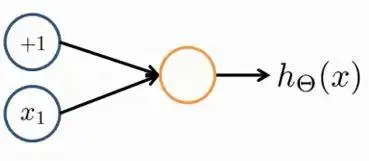
单一神经元的神经网络表示如下图：

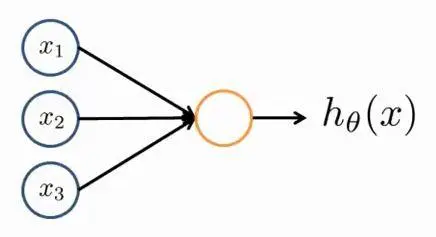
一般只绘制x1,x2,x3,⋯$x_1,x_2,x_3,\cdots$。而x0$x_0$称作偏置单元或偏置神经元，且x0$x_0$总是等于1。

在描述神经元时，将之称为一个有S$S$型函数或逻辑函数作为激励函数的人工神经元。
在神经网络术语中，激励函数是对类似非线性函数g(z)=11+e−z$g(z)=\frac{1}{1+e^{-z}}$的另一个称呼。

模型参数θ=⎡⎣⎢⎢⎢θ0θ1θ2θ3⎤⎦⎥⎥⎥$\theta =\left[\begin{array}{c}{\theta }_0\\ {\theta }_1\\ {\theta }_2\\ {\theta }_3\end{array}\right]$也称权重。

神经网络是由不同的神经元组合在一起：

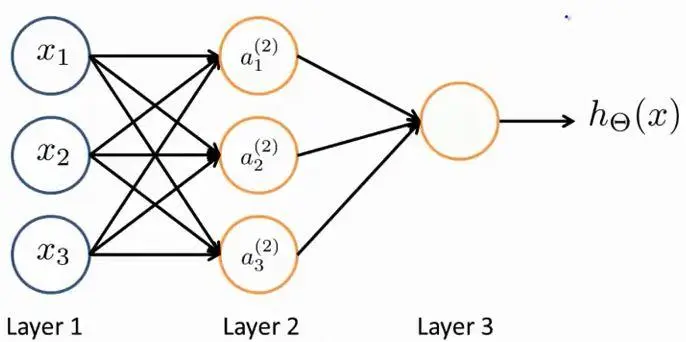
其中，Layer1$Layer1$为输入层，Layer2$Layer2$为隐藏层，Layer3$Layer3$为输出层，Layer1$Layer1$和Layer2$Layer2$可添加偏置单元x0$x_0$及a(2)0$a_0^{(2)}$(值均总为1)，神经网络中可包含多个隐藏层。

a(j)i$a_i^{(j)}$表示第j$j$层的第i$i$个神经元或单元的激励函数，激励函数是指有一个具体神经元读入计算并输出值；
Θ(j)${\mathrm{\Theta }}^{(j)}$为神经网络第j$j$层到第j+1$j+1$层的权重控制矩阵。

如果神经网络中，第j$j$层有sj$s_j$个单元，第j+1$j+1$层有sj+1$s_{j+1}$个单元，则Θ(j)${\mathrm{\Theta }}^{(j)}$为sj+1×(sj+1)$s_{j+1}\times (s_j+1)$维的矩阵。
“+1”来自Θ(j)${\mathrm{\Theta }}^{(j)}$中添加偏置单元x0$x_0$和Θ(j)0${\mathrm{\Theta }}_0^{(j)}$，换句话说，输出节点不包含偏置节点，但输入节点会包括。

令Θ(1)10x0+Θ(1)11x1+Θ(1)12x2+Θ(1)13x3=Z(2)1Θ(1)20x0+Θ(1)21x1+Θ(1)22x2+Θ(1)23x3=Z(2)2Θ(1)30x0+Θ(1)31x1+Θ(1)32x2+Θ(1)33x3=Z(2)3$$\begin{gathered} {\mathrm{\Theta }}_{10}^{(1)}{x}_0+{\mathrm{\Theta }}_{11}^{(1)}{x}_1+{\mathrm{\Theta }}_{12}^{(1)}{x}_2+{\mathrm{\Theta }}_{13}^{(1)}{x}_3=Z_1^{(2)} \\ {\mathrm{\Theta }}_{20}^{(1)}{x}_0+{\mathrm{\Theta }}_{21}^{(1)}{x}_1+{\mathrm{\Theta }}_{22}^{(1)}{x}_2+{\mathrm{\Theta }}_{23}^{(1)}{x}_3=Z_2^{(2)} \\ {\mathrm{\Theta }}_{30}^{(1)}{x}_0+{\mathrm{\Theta }}_{31}^{(1)}{x}_1+{\mathrm{\Theta }}_{32}^{(1)}{x}_2+{\mathrm{\Theta }}_{33}^{(1)}{x}_3=Z_3^{(2)} \end{gathered}$$

则x=⎡⎣⎢⎢⎢x0x1x2x3⎤⎦⎥⎥⎥$x=\left[\begin{array}{c}{x}_0\\ x_1\\ x_2\\ x_3\end{array}\right]$ Z(2)=⎡⎣⎢⎢⎢Z(2)1Z(2)2Z(2)3⎤⎦⎥⎥⎥$Z^{(2)}=\left[\begin{array}{c}{Z}_1^{(2)}\\ Z_2^{(2)}\\ Z_3^{(2)}\end{array}\right]$

⇒Z(2)=Θ(1)x$\Rightarrow Z^{(2)}={\mathrm{\Theta }}^{(1)}x$(x$x$也可以替换成a(1)$a^{(1)}$)
⇒a(2)=g(Z(2))$\Rightarrow a^{(2)}=g(Z^{(2)})$得到a(2)1,a(2)2,a(2)3$a_1^{(2)},a_2^{(2)},a_3^{(2)}$
⇒Adda(2)0=1$\Rightarrow Add{a}_0^{(2)}=1$
⇒Z(3)=Θ(2)a(2)$\Rightarrow Z^{(3)}={\mathrm{\Theta }}^{(2)}{a}^{(2)}$
⇒hΘ(x)=a(3)=g(Z(3))$\Rightarrow h_{\mathrm{\Theta }}(x)=a^{(3)}=g(Z^{(3)})$
整个计算过程称为前向传播

将上述计算过程抽象化：
⇒Z(2)k=Θ(1)k,0x0+Θ(1)k,1x1+Θ(1)k,2x2+⋯+Θ(1)k,nxn$\Rightarrow Z_k^{(2)}={\mathrm{\Theta }}_{k,0}^{(1)}{x}_0+{\mathrm{\Theta }}_{k,1}^{(1)}{x}_1+{\mathrm{\Theta }}_{k,2}^{(1)}{x}_2+\cdots +{\mathrm{\Theta }}_{k,n}^{(1)}{x}_n$
⇒x=⎡⎣⎢⎢⎢x0x1x2x3⎤⎦⎥⎥⎥$\Rightarrow x=\left[\begin{array}{c}{x}_0\\ x_1\\ x_2\\ x_3\end{array}\right]$ Z(j)=⎡⎣⎢⎢⎢Z(j)1Z(j)2Z(j)3⎤⎦⎥⎥⎥$Z^{(j)}=\left[\begin{array}{c}{Z}_1^{(j)}\\ Z_2^{(j)}\\ Z_3^{(j)}\end{array}\right]$
⇒$\Rightarrow$令x=a(1)→Z(j)=Θ(j−1)a(j−1)$x=a^{(1)}\to Z^{(j)}={\mathrm{\Theta }}^{(j-1)}{a}^{(j-1)}$
⇒a(j)=g(Z(j))$\Rightarrow a^{(j)}=g(Z^{(j)})$在a(j)$a^{(j)}$中增加偏置单元a(j)0=1$a_0^{(j)}=1$
⇒Z(j+1)=Θ(j)a(j)$\Rightarrow Z^{(j+1)}={\mathrm{\Theta }}^{(j)}{a}^{(j)}$
⇒hΘ(x)=a(j+1)=g(Z(j+1))$\Rightarrow h_{\mathrm{\Theta }}(x)=a^{(j+1)}=g(Z^{(j+1)})$

应用举例：
利用神经网络计算y=x1 AND x2$y=x_{1}AND{x}_2$其中x1,x2∈{0,1}$x_1,x_2\in \{0,1\}$

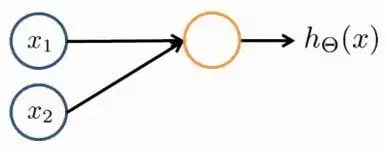
加上偏置单元，上图变化如下：

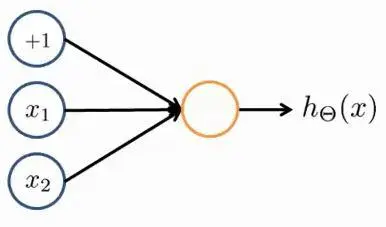
Θ(1)=[−302020]${\mathrm{\Theta }}^{(1)}=[-302020]$
则：hΘ(x)=g(−30+20x1+20x2)$h_{\mathrm{\Theta }}(x)=g(-30+20x_1+20x_2)$
在g(z)$g(z)$函数中，当z=4.6$z=4.6$时，g(z)=0.99≈1$g(z)=0.99\approx 1$；当z=−4.6$z=-4.6$时，g(z)=0.01≈0$g(z)=0.01\approx 0$
所以：

同理：
利用神经网络计算y=x1 OR x2$y=x_{1}OR{x}_2$其中x1,x2∈{0,1}$x_1,x_2\in \{0,1\}$
Θ(1)=[−102020]${\mathrm{\Theta }}^{(1)}=[-102020]$
利用神经网络计算y=x1 NOR x2$y=x_{1}NOR{x}_2$其中x1,x2∈{0,1}$x_1,x_2\in \{0,1\}$
Θ(1)=[10−20−20]${\mathrm{\Theta }}^{(1)}=[10-20-20]$

利用神经网络计算y=NOT x1$y=NOT{x}_1$其中x1∈{0,1}$x_1\in \{0,1\}$

Θ(1)=[10−20]${\mathrm{\Theta }}^{(1)}=[10-20]$
则：hΘ(x)=g(10−20x1)$h_{\mathrm{\Theta }}(x)=g(10-20x_1)$