位置计数系统

位置计数系统

以我们现实生活中的一个数字为例，它代表了什么意义。
678 = 6个100 + 7个10 + 8个1
$678 = 6 \times 10^2 + 7 \times 10^1 + 8 \times 10^0$678=6×102+7×101+8×100
但是上述的说法对吗？既对也不对，因为它没有说明我们应该采用的基数是什么，也就是说，上面的是以直接将10作为基数，由于我们并未说明它是10进制数。假如它的基数是16那么他代表的数字就不是上面的答案了。

• 基数(base)
  计数系统中的基本值，规定了这个系统中所使用的数字量和数位位置的值。
• 位置计数法
  一种表达数字的系统，数位按照顺序排列，每个数位有一个位值，数字的值就是每个数位和位值的乘积之和。在这个系统中数字是这样表示的：
  $n ={\pm(S_{k-1} \cdots S_2S_1S_0S_{-1}S_{-2} \cdots S_{-l})}_b$n=±(Sk−1​⋯S2​S1​S0​S−1​S−2​⋯S−l​)b​
  它的值是：
  $n = {\pm (S_{k-1} \times b^{k-1} + S_{k-2} \times b^{k-2} \cdots S_1 \times b^1 + S_0 \times b^{0} + S_{-1} \times b^{-1} + S_{-2} \times b^{-2} + S_{-l} \times b^{-l} )}$n=±(Sk−1​×bk−1+Sk−2​×bk−2⋯S1​×b1+S0​×b0+S−1​×b−1+S−2​×b−2+S−l​×b−l)

其中$S$S是符号集。$b$b是基数，$S_i$Si​指的是该符号的位置为 $i$i 。$b$b的非负数幂跟整数有关，$b$b的负数幂跟小数有关。其中 $k$k 的的取值从0开始，$l$l 的取值从 -1 开始

1.十进制系统 b = 10

在十进制系统中，$S = {\lbrace 0, 1, \cdots, 8, 9} \rbrace$S={0,1,⋯,8,9} 。数字写为
$n ={\pm(S_{k-1} \cdots S_2S_1S_0S_{-1}S_{-2} \cdots S_{-l})}_{10}$n=±(Sk−1​⋯S2​S1​S0​S−1​S−2​⋯S−l​)10​
其中，$S_i$Si​是数码，$b = 10$b=10是基底，$k$k是数码的量。也可以理解为不同的数码在不同的位置上有不同的权重。

例1：+123 使用位置系统表示为：

$N = +(1 \times 10^2 + 2 \times 10^1 + 3 \times 10^0)$N=+(1×102+2×101+3×100)
在此处，可以认为1的数码权重为100, 2的权重为10，3的权重为1。

例2：-25.67

$R = -(2 \times 10^1 + 5 \times 10^0 + 6 \times 10^{-1} + 7 \times 10^{-1})$R=−(2×101+5×100+6×10−1+7×10−1)

2. 二进制系统 b = 2

在二进制系统中，$S = {\lbrace 0, 1} \rbrace$S={0,1} 。数字写为
$n ={\pm(S_{k-1} \cdots S_2S_1S_0S_{-1}S_{-2} \cdots S_{-l})}_{2}$n=±(Sk−1​⋯S2​S1​S0​S−1​S−2​⋯S−l​)2​

例1：与$({25})_{10}$(25)10​等值的二进制数$({11001})_2$(11001)2​

$N = (1 \times 2^4 + 1 \times 2^3 + 0 \times 2^{2} + 0 \times 2^{1} + 1 \times 2^0)$N=(1×24+1×23+0×22+0×21+1×20)

例2：$({5.75})_{10}$(5.75)10​等值的二进制数$({101.11})_2$(101.11)2​

$N = (1 \times 2^2 + 0 \times 2^{1} + 1 \times 2^{0} + 1 \times 2^{-1} + 1 \times 2^{-2})$N=(1×22+0×21+1×20+1×2−1+1×2−2)

3 进制之间的相互转换

3.1 其他进制到10进制

将数码乘以原系统中的位置量求和，便可得到10进制数。

例1

$({111.101})_2$(111.101)2​转换为10进制数：
$R = (1 \times 2^2 + 1 \times 2^3 + 0 \times 2^{1} + 1 \times 2^{0} + 1 \times 2^{-1} + 0 \times 2^{-2} + 0 \times 2^{-3}) = 7.625$R=(1×22+1×23+0×21+1×20+1×2−1+0×2−2+0×2−3)=7.625

3.2 10进制转换为其他进制

整数部分采用：连除法；小数部分采用连乘法。

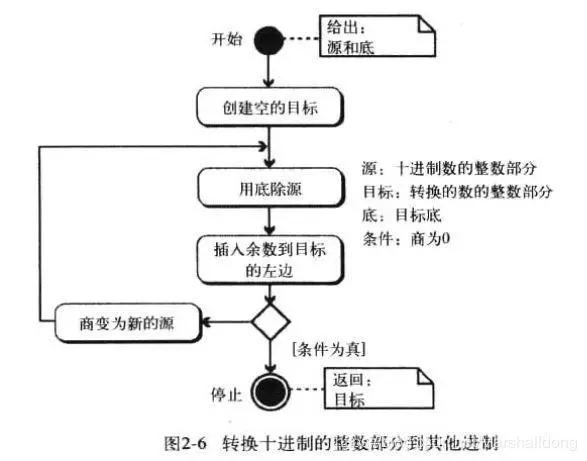
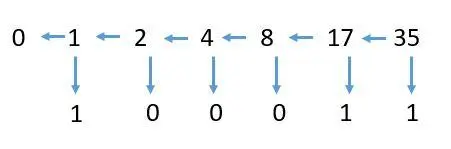
例1：$({35})_{10}$(35)10​转换为二进制

一边连续除2得到商和余数一边左移。

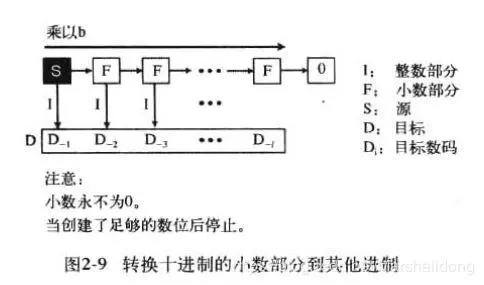
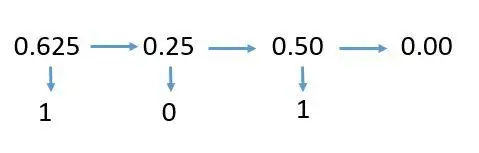
例2：$({0.625})_{10}$(0.625)10​转换为二进制

连续乘2，整数部分拿去，然后继续乘2，直到满足精度或者为0。
0.625 * 2 = 1.25 取整 $\Rightarrow$⇒ 1 余数$\Rightarrow$⇒ 0.25
0.25 *2 = 0.5 取整 $\Rightarrow$⇒ 0 余数$\Rightarrow$⇒ 0.5
0.5 *2 = 1 取整 $\Rightarrow$⇒ 1 余数$\Rightarrow$⇒ 0

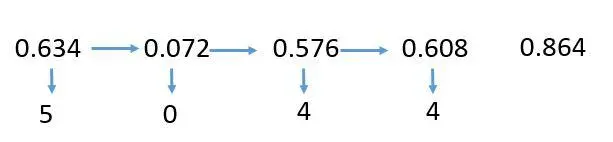
例3：$({0.634})_{10}$(0.634)10​转换为8进制，且精确到小数4位：

参考文献

《计算机科学导论》第三版

本人联系方式（添加请说明来由）：
Email：[email protected]
QQ: 1289490664