线性回归--机器学习
线性回归 -- LIner regression
线性回归(Linear regression)是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析 —*
线性回归--理论推导
<1> 数据: 本次推导使用的数据为--银行贷款数据。
<2> 假设: 假设工资参数为θ1, 年龄参数为θ2。
拟合平面:
整合:
注: 此时的整合中的x = (x0 x1 x2 ... xn), x0是新加入的值,为了保证θ0起作用,则x0 = 1。为什么要进行加入x0这步操作呢?其实就是为了化简表达式, 使的可以使用矩阵来进行表示。
<3> 误差分析(重点):
真实值与预测值之间一定存在误差(用ε来表示误差)
对于每一个样本 ( y(i)为真实值, θT为参数矩阵, x(i)为第i挑数据的属性内容矩阵, ε(i)为第i条数据所产生的误差)
(红色的点表示真实值, 垂线与平面交点为预测值,高度差代表误差)
高斯分布也就是正态分布
独立: 假如张三和李四都到银行进行贷款,银行不会因为张三和李四认识而改变银行贷款的标准,即张三和李四为样本, 银行则为算法, 所以每个样本之间是独立的。
相同分布: 假如张三去的是建设银行, 而李四去的是农业银行, 两个不同的数据混合在一块去建立一个用来预测的模型, 这不符合逻辑。 我们要建立一个模型,要么是建设银行的模型, 要么是农业银行的模型, 即概括为数据要在相同的分布下,建立的模型才有实际意义。
均值为0: 如银行贷款时, 有时会给你多贷一些, 有时会给你少贷一些, 但不可能一直给你多贷或者少贷, 所以多贷 与少贷的均值趋近于0
高斯分布: 在高斯分布中, 越靠近0的位置, 产生的偏差越小, 出现的概率就越大; 越远离0的位置, 产生的偏差越 大, 出现的概率就越小。(最大似然估计就是从此处的概率得出, 此处越接近0, 概率p越大)
高斯分布: (主要分布在(-1,1)之间)
在机器学习中, 会进行很多假设, 并以这种假设进行推导, 最终得到的结果是可以利用的, 只要最终得到的模型可用, 即可以说假设成立的, 因为没有完全独立和完全相同的分布, 假设是机器学习解决问题的办法。
线性回归--公式推导
<1> 公式代换:
<2> 似然函数与对数似然
似然函数: 似然函数是根据样本去估计参数的值的一个函数, 即是由数据去计算参数的大小为多大时, 参数和我们的数据组合后更接近真实值。(总而言之, 似然函数就是为了求解参数的函数)
对数似然: 对数似然相对于似然函数的有点在于运算方便。似然函数求取的方法是迭乘, 数字较大时会很不方便;对数似然求取的方法是迭加。(相比于似然函数而言, 对数似然较为实用)
<3> 目标函数:
在进行对数运算进行展开化简
极大似然估计: 极大似然估计即L(θ)或ln(L(θ))越大越好, 然而化简后 > 0, 且为一个定值。所以要使的
越小越好, 这样得到的参数的准确率就越高。又因为
为定值, 所以使的后半部分
越小即可。这样可以根据
表达式构成一个目标函数。
<4> 公式推导:
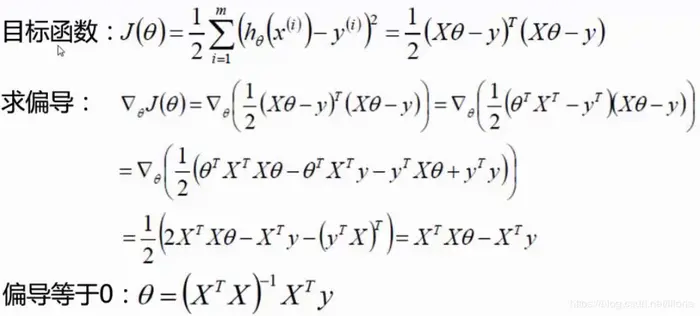
已知数据个数为:m, 数据属性为:d, 因为X矩阵增加了一列x0 = 1, 所以X矩阵为一个m*(d + 1)的矩阵, θ矩阵为(d + 1)*1的矩阵(列向量矩阵), y矩阵为m*1的矩阵。
X = [[x10 x11 ... x1d]
[x20 x21 ... x2d]
... ... ... ...
[xm0 xm1 ... xmd]]
θ = [θ0
θ1
...
θd]
y = [y0
y1
...
ym]
到此处已经把相应属性的参数以及偏置项都解出, 可以根据此回归参数来预测未知数据, 将位置数据的内容矩阵加上一列值为1, 即x0 = 1, 就可以求的预测值。
注: 此处的hθ是先前介绍的拟合平面, 一些矩阵的运算下一步解释
<5> 矩阵的平方、求导:
矩阵的平方: 假设矩阵A,A2(A矩阵的平方) = AT(A矩阵的转置矩阵) * A
矩阵的求导法则:
