ML模型3：逻辑回归模型

逻辑回归模型

逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法，运用梯度下降来求解参数，来达到将数据二分类的目的。

1. 问题引入

线性回归是进行回归学习，但如果要做分类任务该怎么办呢？

在广义线性模型下，可以利用一个单调可微的函数将分类任务的标签y与线性回归模型的预测结果联系起来。

实值z → 0/1值？（Q1. 逻辑回归和线性回归有什么区别？）

选用理想的单位阶跃函数 → 单位阶跃函数不连续 → 寻找替代函数 - 对数几率函数(sigmoid函数)
$g(z) = \frac{1}{1+e^{-z}}$g(z)=1+e−z1​
下图所示 - 红色单位阶跃函数/黑色sigmoid函数

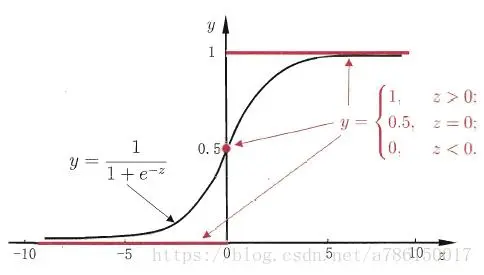
注：以下以常见的二分类为例。且样本集和线性回归相似，只是输出y为离散值。

2. 模型描述

Sigmoid函数：
$g(z) = \frac{1}{1+e^{-z}}$g(z)=1+e−z1​

令$z = x\theta$z=xθ，得到逻辑回归的一般形式：
${h_\theta }(x;\theta ) = {1 \over {1 + {e^{ - x\theta }}}}$hθ​(x;θ)=1+e−xθ1​

逻辑回归的基本假设 - 假设数据服从伯努利分布。

伯努利分布的简单例子就是抛硬币：抛中为正面的概率是p，抛中为反面的概率是1−p。

即
$P(y = 1|x;\theta ) = {h_\theta }(x) = {1 \over {1 + {e^{ - x\theta }}}}$P(y=1∣x;θ)=hθ​(x)=1+e−xθ1​$P(y = 0|x;\theta ) = 1 - {h_\theta }(x) = 1 - {1 \over {1 + {e^{ - x\theta }}}}$P(y=0∣x;θ)=1−hθ​(x)=1−1+e−xθ1​

3. 损失函数

损失函数是基于最大似然估计推导得到的。

1）综合上述输入$x$x下分类结果0/1的概率，得：
$P(y|x;\theta ) = {\left( {{h_\theta }(x)} \right)^y}{\left( {1 - {h_\theta }(x)} \right)^{1 - y}}$P(y∣x;θ)=(hθ​(x))y(1−hθ​(x))1−y
2）取似然函数为：
$\begin{aligned} L\left( \theta \right) &= \prod\limits_{i = 1}^m {P\left( {{y^{\left( i \right)}}|{x^{\left( i \right)}};\theta } \right)} \\ &= \prod\limits_{i = 1}^m {{{\left( {{h_\theta }({x^{\left( i \right)}})} \right)}^{{y^{\left( i \right)}}}}{{\left( {1 - {h_\theta }({x^{\left( i \right)}})} \right)}^{1 - {y^{\left( i \right)}}}}} \end{aligned}$L(θ)​=i=1∏m​P(y(i)∣x(i);θ)=i=1∏m​(hθ​(x(i)))y(i)(1−hθ​(x(i)))1−y(i)​
3）对数似然函数为：
$\begin{aligned} l\left( \theta \right)&=\log L\left( \theta \right)\\ &= \sum\limits_{i = 1}^m {\left[ {{y^{\left( i \right)}}\log {h_\theta }\left( {{x^{\left( i \right)}}} \right) + \left( {1 - {y^{\left( i \right)}}} \right)\log \left( {1 - {h_\theta }\left( {{x^{\left( i \right)}}} \right)} \right)} \right]} \end{aligned}$l(θ)​=logL(θ)=i=1∑m​[y(i)loghθ​(x(i))+(1−y(i))log(1−hθ​(x(i)))]​

最大似然估计就是求得使$l\left( \theta \right)$l(θ)取最大值时的 $\theta$θ，这里可以使用梯度上升法求解，求得的 $\theta$θ 就是要求的最佳参数。

4）为了统一用梯度下降法求解，通常将损失函数定义如下：（Q2. 为什么要除以样本数m？）
$\begin{aligned} J\left( \theta \right) &= - {1 \over m}l\left( \theta \right)\\ &= - {1 \over m}\sum\limits_{i = 1}^m {\left[ {{y^{\left( i \right)}}\log {h_\theta }\left( {{x^{\left( i \right)}}} \right) + \left( {1 - {y^{\left( i \right)}}} \right)\log \left( {1 - {h_\theta }\left( {{x^{\left( i \right)}}} \right)} \right)} \right]} \end{aligned}$J(θ)​=−m1​l(θ)=−m1​i=1∑m​[y(i)loghθ​(x(i))+(1−y(i))log(1−hθ​(x(i)))]​

4. 模型求解

显然逻辑回归最终拟合函数是非线性的（sigmoid函数分线性），所以此处选择用迭代法-梯度下降法求解。

1）输入：损失函数 $J\left( \theta \right) = - {1 \over m}\sum\limits_{i = 1}^m {\left[ {{y^{\left( i \right)}}\log {h_\theta }\left( {{x^{\left( i \right)}}} \right) + \left( {1 - {y^{\left( i \right)}}} \right)\log \left( {1 - {h_\theta }\left( {{x^{\left( i \right)}}} \right)} \right)} \right]}$J(θ)=−m1​i=1∑m​[y(i)loghθ​(x(i))+(1−y(i))log(1−hθ​(x(i)))]
初始值 $\theta$θ 和学习步长 $\alpha$α

2）更新方程：
${\theta _j} = {\theta _j} - \alpha {\partial \over {\partial {\theta _j}}}J\left( \theta \right),\left( {j = 0,1...n} \right)$θj​=θj​−α∂θj​∂​J(θ),(j=0,1...n)

3）损失函数的梯度计算如下：
$\begin{aligned} {\partial \over {\partial {\theta _j}}}J\left( \theta \right) &= - {1 \over m}\sum\limits_{i = 1}^m {\left[ {{y^{\left( i \right)}}{1 \over {{h_\theta }\left( {{x^{\left( i \right)}}} \right)}}{\partial \over {\partial {\theta _j}}}{h_\theta }\left( {{x^{\left( i \right)}}} \right) - \left( {1 - {y^{\left( i \right)}}} \right){1 \over {1 - {h_\theta }\left( {{x^{\left( i \right)}}} \right)}}{\partial \over {\partial {\theta _j}}}{h_\theta }\left( {{x^{\left( i \right)}}} \right)} \right]}\\ &= - {1 \over m}\sum\limits_{i = 1}^m {\left[ {{y^{\left( i \right)}}{1 \over {g\left( {{x^{\left( i \right)}}\theta } \right)}} - \left( {1 - {y^{\left( i \right)}}} \right){1 \over {1 - g\left( {{x^{\left( i \right)}}\theta } \right)}}} \right]} {\partial \over {\partial {\theta _j}}}g\left( {{x^{\left( i \right)}}\theta } \right)\\ &=- {1 \over m}\sum\limits_{i = 1}^m {\left[ {{y^{\left( i \right)}}{1 \over {g\left( {{x^{\left( i \right)}}\theta } \right)}} - \left( {1 - {y^{\left( i \right)}}} \right){1 \over {1 - g\left( {{x^{\left( i \right)}}\theta } \right)}}} \right]} g\left( {{x^{\left( i \right)}}\theta } \right)\left( {1 - g\left( {{x^{\left( i \right)}}\theta } \right)} \right)x_j^{\left( i \right)}\\ &= - {1 \over m}\sum\limits_{i = 1}^m {\left[ {{y^{\left( i \right)}}\left( {1 - g\left( {{x^{\left( i \right)}}\theta } \right)} \right) - \left( {1 - {y^{\left( i \right)}}} \right)g\left( {{x^{\left( i \right)}}\theta } \right)} \right]} x_j^{\left( i \right)}\\ &= - {1 \over m}\sum\limits_{i = 1}^m {\left[ {{y^{\left( i \right)}} - g\left( {{x^{\left( i \right)}}\theta } \right)} \right]} x_j^{\left( i \right)}\\ &= - {1 \over m}\sum\limits_{i = 1}^m {\left[ {{y^{\left( i \right)}} - {h_\theta }\left( {{x^{\left( i \right)}}} \right)} \right]} x_j^{\left( i \right)}\\ &= {1 \over m}\sum\limits_{i = 1}^m {\left[ {{h_\theta }\left( {{x^{\left( i \right)}}} \right) - {y^{\left( i \right)}}} \right]} x_j^{\left( i \right)} \end{aligned}$∂θj​∂​J(θ)​=−m1​i=1∑m​[y(i)hθ​(x(i))1​∂θj​∂​hθ​(x(i))−(1−y(i))1−hθ​(x(i))1​∂θj​∂​hθ​(x(i))]=−m1​i=1∑m​[y(i)g(x(i)θ)1​−(1−y(i))1−g(x(i)θ)1​]∂θj​∂​g(x(i)θ)=−m1​i=1∑m​[y(i)g(x(i)θ)1​−(1−y(i))1−g(x(i)θ)1​]g(x(i)θ)(1−g(x(i)θ))xj(i)​=−m1​i=1∑m​[y(i)(1−g(x(i)θ))−(1−y(i))g(x(i)θ)]xj(i)​=−m1​i=1∑m​[y(i)−g(x(i)θ)]xj(i)​=−m1​i=1∑m​[y(i)−hθ​(x(i))]xj(i)​=m1​i=1∑m​[hθ​(x(i))−y(i)]xj(i)​​

其中第一个等号用到下式：
${\partial \over {\partial {\theta _j}}}\log {h_\theta }\left( {{x^{\left( i \right)}}} \right){\rm{ = }}{1 \over {{h_\theta }\left( {{x^{\left( i \right)}}} \right)}}{\partial \over {\partial {\theta _j}}}{h_\theta }\left( {{x^{\left( i \right)}}} \right)$∂θj​∂​loghθ​(x(i))=hθ​(x(i))1​∂θj​∂​hθ​(x(i))
${\partial \over {\partial {\theta _j}}}\log \left( {1 - {h_\theta }\left( {{x^{\left( i \right)}}} \right)} \right) = - {1 \over {1 - {h_\theta }\left( {{x^{\left( i \right)}}} \right)}}{\partial \over {\partial {\theta _j}}}{h_\theta }\left( {{x^{\left( i \right)}}} \right)$∂θj​∂​log(1−hθ​(x(i)))=−1−hθ​(x(i))1​∂θj​∂​hθ​(x(i))
第三个等号用到下式：
$g(z) = {1 \over {1 + {e^{ - z}}}}$g(z)=1+e−z1​
$g'(z) = {{{e^{ - z}}} \over {{{\left( {1 + {e^{ - z}}} \right)}^2}}} = g(z)\left( {1 - g(z)} \right)$g′(z)=(1+e−z)2e−z​=g(z)(1−g(z))
${\partial \over {\partial {\theta _j}}}g\left( {{x^{\left( i \right)}}\theta } \right) = g\left( {{x^{\left( i \right)}}\theta } \right)\left( {1 - g\left( {{x^{\left( i \right)}}\theta } \right)} \right)x_j^{\left( i \right)}$∂θj​∂​g(x(i)θ)=g(x(i)θ)(1−g(x(i)θ))xj(i)​

4）最终更新方程为：
$\begin{aligned} {\theta _j} &= {\theta _j} - \alpha {\partial \over {\partial {\theta _j}}}J\left( \theta \right)\\ &= {\theta _j} - {\alpha \over m}\sum\limits_{i = 1}^m {\left[ {{h_\theta }\left( {{x^{\left( i \right)}}} \right) - {y^{\left( i \right)}}} \right]} x_j^{\left( i \right)} \end{aligned}$θj​​=θj​−α∂θj​∂​J(θ)=θj​−mα​i=1∑m​[hθ​(x(i))−y(i)]xj(i)​​，其中${j = 0,1...n}$j=0,1...n

直到$\Delta \theta$Δθ小于阈值$\varepsilon$ε
$\Delta \theta {\rm{ = }}{\partial \over {\partial \theta }}J\left( \theta \right) &lt; \varepsilon$Δθ=∂θ∂​J(θ)<ε

5. 向量化表示

（面试题）

更新方程为：
$\theta = \theta - {\alpha \over m}{x^T}\left( {{1 \over {1 + {e^{ - x\theta }}}} - y} \right)$θ=θ−mα​xT(1+e−xθ1​−y)
Trick：可以用矩阵维数来判断向量化表示应该如何写。$x$x是$m \times n$m×n维，$\theta$θ是$n \times 1$n×1维，$y$y是$m \times 1$m×1维。

$x = \begin{bmatrix} x_1^{\left( 0 \right)} &amp; x_2^{\left( 0 \right)} &amp; ... &amp; x_n^{\left( 0 \right)} \\ x_1^{\left( 1 \right)} &amp; x_2^{\left( 1 \right)} &amp; ... &amp; x_n^{\left( 1 \right)} \\ ... &amp; ... &amp; ... &amp; ... \\ x_1^{\left( m \right)} &amp; x_2^{\left( m \right)} &amp; ... &amp; x_n^{\left( m \right)} \end{bmatrix}，y = \begin{bmatrix} y^{\left( 0 \right)} \\ y^{\left( 1 \right)} \\ ... \\ y^{\left( m \right)} \end{bmatrix}$x=⎣⎢⎢⎢⎡​x1(0)​x1(1)​...x1(m)​​x2(0)​x2(1)​...x2(m)​​............​xn(0)​xn(1)​...xn(m)​​⎦⎥⎥⎥⎤​，y=⎣⎢⎢⎡​y(0)y(1)...y(m)​⎦⎥⎥⎤​
$\theta = {({\theta _0},{\theta _1},...,{\theta _n})^T}$θ=(θ0​,θ1​,...,θn​)T

6. 逻辑回归模型-优缺点分析

优点：简单易用，易理解；

缺点：准确率并不是很高；很难处理数据不平衡的问题（注意选取合适的评价指标）

7. Code

from sklearn import linear_model
clf = linear_model.LogisticRegression(C=1.0, penalty='l1', tol=1e-6)

参数解释
C - 正则项权重
penalty - 可选择为"l1"和"l2"，分别对应L1和L2正则化，默认是L2正则化
tol - 截止条件，$\Delta \theta$Δθ的阈值$\varepsilon$ε

8. 拓展 - 其他知识点

**函数选择sigmoid函数 - 梯度消失/梯度爆炸
优化方法和正则化需详解（同线性回归）
学习步长的选择

Q&A

Q1. 逻辑回归和线性回归有什么区别？（面试题）

预测结果 - 线性回归的预测结果是连续的，逻辑回归的结果是离散的；
假设函数 - 逻辑回归在线性回归的实数范围输出上施加了sigmoid函数，将值收敛在0-1之间；
损失函数 - 线性回归是差平方和，逻辑回归是对数似然函数。

Q2. 为什么要除以样本数m？（面试题）

数量越多误差越大，所以平滑一下

Q3. 关于损失函数的选择

1. 为什么要用对数损失函数作为损失函数？

损失函数一般有四种：平方损失函数/对数损失函数/HingeLoss0-1损失函数/绝对值损失函数。
对极大似然函数取对数可以推得对数损失函数。
${\theta _j} = {\theta _j} - {\alpha \over m}\sum\limits_{i = 1}^m {\left[ {{h_\theta }\left( {{x^{\left( i \right)}}} \right) - {y^{\left( i \right)}}} \right]} x_j^{\left( i \right)}$θj​=θj​−mα​i=1∑m​[hθ​(x(i))−y(i)]xj(i)​
从上式可以看出，逻辑回归模型下，对数损失函数的训练求解参数的速度是比较快的。因为${\theta _j}$θj​的更新速度只和$x_j^{\left( i \right)}$xj(i)​，${{y^{\left( i \right)}}}$y(i)相关，和sigmoid函数本身的梯度无关。这样更新的速度是可以自始至终都比较稳定。

2. 为什么不选平方损失函数的呢？

如果使用平方损失函数，会发现梯度更新的速度和sigmoid函数本身的梯度是很相关的。sigmoid函数在它在定义域内的梯度都不大于0.25。这样训练会非常的慢。

Q4.逻辑回归在训练的过程中，如果有很多的特征高度相关/有一个特征重复了很对遍，会造成怎样的影响？

如果损失函数最终收敛，就算有很多特征高度相关也不会影响分类器的效果。
但我们通常选择去掉高度相关的特征，因为这样会让模型的可解释性更好，也会加快训练速度。

Ref
机器学习–Logistic回归计算过程的推导
逻辑回归的常见面试点总结