根据两点的经纬度求方位角和距离等问题

自动驾驶中利用gps算距离和方位角的问题是非常基本的问题也很常见。主要涉及到的就是球面三角学。

本文参考这篇文章做一个说明，这一篇其实也是转载，原创的博文已经不见了。原来转载的那篇文章有一些错误，格式排版也不是很好，所以此篇博客稍微整理了一下。
在这篇博客中主要解决三个问题：

1. 已知两点经纬度，求两点间距离；
2. 已知两点经纬度，求一点相对于另一点航向；
3. 已知一点经纬度及与另一点距离和航向，求另一点经纬度；

总声明：

因为地球偏心率极低，所以此处将地球看做球体，以下所有公式在适用范围内使用可以保证计算结果与WGS84坐标系统下测量的偏差最大不超过0.5%。关于度娘知道上有人说的需要将WGS84坐标转换成北京54、西安80后再计算的高深言论，我的观点是：只要不是搞大地测量、土木工程、导弹发射或者载人飞船回收，就根本就没有必要那么做，请这帮满嘴专业词汇自己却连WGS84坐标系统下距离求算公式都给不出的砖家们“地平线有多远，就给我滚多远”。关于方法的名称，是为便于编写自己起的，请勿当做正式名称与人讨论。因本人才浅手拙，不善算数，故错误难免，如有发现，定及时改正，请见谅。

有关WGS84坐标系统下的距离及航向求算方法，需要精确计算的请点击下列查看
距离及航向1
距离及航向2
Vincenty公式
更多信息，请谷歌 Vincenty’s formula

关于WGS84坐标系统，请点下列查看：
WGS84 1
WGS84 2

在求算前我们先对符号及单位进行约定：

$此处设定求B相对于A的航向，即A为当前位置，B为目标位置$此处设定求B相对于A的航向，即A为当前位置，B为目标位置

$Aj：A点经度$Aj：A点经度

$Aw：A点纬度$Aw：A点纬度

$Bj：B点经度$Bj：B点经度

$Bw：B点纬度$Bw：B点纬度

北纬为正，南纬为负；东经为正，西经为负

经纬度使用十进制度，i.e.DDD.DDDDDD°，非度分或度分秒。

度数未加说明均采用角度制

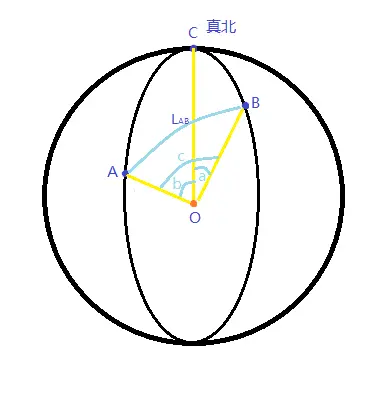
$A,B,C表示球面上的三个点及球面上“弧线”在该点处所夹的角，C所处位置为北极点$A,B,C表示球面上的三个点及球面上“弧线”在该点处所夹的角，C所处位置为北极点

$a,b,c表示A,B,C三点的对“弧”两端点与地心连线所夹的角（其实这里解释成ABC三点对弧的弧度更方便）$a,b,c表示A,B,C三点的对“弧”两端点与地心连线所夹的角（其实这里解释成ABC三点对弧的弧度更方便）

$O$O：球心

$L：AB两点间球面距离，也叫做大圆距离，即过AOB三点的平面与球相交所产生的圆弧中劣弧AB的长度$L：AB两点间球面距离，也叫做大圆距离，即过AOB三点的平面与球相交所产生的圆弧中劣弧AB的长度

$R：地球平均半径$R：地球平均半径

$Bearing：起始真航向，也叫大圆始航向。以真北为0度起点，由东向南向西顺时针旋转360度。$Bearing：起始真航向，也叫大圆始航向。以真北为0度起点，由东向南向西顺时针旋转360度。

此处所要求算的角度非“地理相对方位”，而是“航行方向”也就是“圆弧L在A点处的切线与真北方向的夹角”。举个栗子：设A点经纬度：40°N,10°E；B点经纬度：40°N，100°E。显然B点在A点的正东方90°，但是如果某人自A点以最短距离去B点，则在A点需要先向57.2676°方向走，之后逐渐变化航向（只是所测得的航向发生了变化，但他仍然在那一个大圆平面上），最终到达B点时的行走方向为122.7324°。这里，57.2676°就是我所说“起始真航向”。与这个概念相对的另一个航向叫做恒向线航向，更多详情请谷歌：Rhumb line，目前暂不讨论恒向线距离及恒向线航向求算的问题.

（注：因我考虑欠缺，没有注意字母C大小写较难分辨，所以此处提醒读者在后面的公式中注意C的大小写。

对于一些GPS接收机，其数据格式为NMEA-0183，经纬度报文样式为DDDMM.MMMM，需要将它转换为十进制度，公式为：

经纬度（度）=DDD+MM.MMMM/60）

一、距离的求算

方法1、球面余弦公式法

适用范围：理论上，此方法适用于球面上任意两点间的距离求算，但是因为公式中有cos项，当系统的浮点运算精度不高时，在求算较近的两点间的距离时会有较大误差（64位系统一般无需担心此问题）。

已知：$Aj$Aj，$Aw$Aw，$Bj$Bj，$Bw$Bw，$R$R

求算：

第一步：在知道AB点经纬度后，要用到第一个公式，球面余弦公式，

$cos(c)=cos(a)*cos(b)+sin(a)*sin(b)*cos(c)$cos(c)=cos(a)∗cos(b)+sin(a)∗sin(b)∗cos(c)

这里，角C等于角A-OC-B，也就是面AOC与面BOC的二面角，也就是$Bj-Aj$Bj−Aj

这里我们将已知数据代入，公式便写成：

$cos(c)=cos(90-Bw)*cos(90-Aw)+sin(90-Bw)*sin(90-Aw)*cos(Bj-Aj)$cos(c)=cos(90−Bw)∗cos(90−Aw)+sin(90−Bw)∗sin(90−Aw)∗cos(Bj−Aj)

求得c的余弦值后用反余弦函数便可求得角c

$c=arccos(cos(90-Bw)*cos(90-Aw)+sin(90-Bw)*sin(90-Aw)*cos(Bj-Aj))$c=arccos(cos(90−Bw)∗cos(90−Aw)+sin(90−Bw)∗sin(90−Aw)∗cos(Bj−Aj))

将角度化为弧度后求取距离
$rad(c)=\frac{c}{180}*\pi$rad(c)=180c​∗π
$L=R*rad(c)$L=R∗rad(c)
这里要注意，L的单位与R的单位时一致的，单位不同的不要忘记换算。另外最后的Bj-Aj的顺序在这里就无所谓，因为cos函数的Y轴对称性值都是一样的。

方法2、Haversine法

适用范围：此方法适用于球面上任意两点间的距离求算，用高中数学知识即可证明此方法是球面余弦函数的一个变换，因为其中换掉了cos项，因此不存在短距离求算时对系统计算精度的过多顾虑的问题。

已知：$Aj$Aj，$Aw$Aw，$Bj$Bj，$Bw$Bw，$R$R

求算：

将已知数据代入，公式写为
$L=2*R*arcsin(\sqrt{sin^2(\frac{Bw-Aw}{2})+cos(Aw)*cos(Bw)*sin^2(\frac{Bj-Aj}{2})})$L=2∗R∗arcsin(sin2(2Bw−Aw​)+cos(Aw)∗cos(Bw)∗sin2(2Bj−Aj​)​)
这里为书写方便默认上式反正弦函数求取度数为弧度制。这是一个非常重要的公式，基本上gps求解距离的问题都是用的此公式！
关于这个公式的推导，请点此：Haversine formula
更多关于此方法的介绍，请谷歌 Haversine

方法3、直角坐标系法

适用范围：因为将球坐标转化为直角坐标并运用勾股定理，所以只能在两点相聚较近时使用，纬度越高，使用范围越窄。

已知：$Aj，Aw，Bj，Bw，R$Aj，Aw，Bj，Bw，R

求算：

简化算法的基本思路就是将以经纬度表示的球坐标转换成三维直角坐标，再利用立体几何知识去解决。

设：$Xa、Ya、Za为三维直角坐标下A点的坐标，B点坐标同样式，$Xa、Ya、Za为三维直角坐标下A点的坐标，B点坐标同样式，

$Ha为A点海拔高度，Hb为b点海拔高度$Ha为A点海拔高度，Hb为b点海拔高度

则

$Xa=(R+Ha)×cos(Aw)×cos(Aj)$Xa=(R+Ha)×cos(Aw)×cos(Aj)

$Ya=(R+Ha)×cos(AW)×sin(Aj)$Ya=(R+Ha)×cos(AW)×sin(Aj)

$Za=(R+Ha)×sin(Aw)$Za=(R+Ha)×sin(Aw)

$Xb=(R+Hb)×cos(Bw)×cos(Bj)$Xb=(R+Hb)×cos(Bw)×cos(Bj)

$Yb=(R+Hb)×cos(Bw)×sin(Bj)$Yb=(R+Hb)×cos(Bw)×sin(Bj)

$Zb=(R+Hb)×sin(Bw)$Zb=(R+Hb)×sin(Bw)

（注：此处坐标转换为诱导公式化简后的形式，关于球坐标转直角坐标的公式可点此查看：球坐标转直角坐标）

$\Delta X=Xa-Xb$ΔX=Xa−Xb $\Delta Y=Ya-Yb$ΔY=Ya−Yb $\Delta Z=Za-Zb$ΔZ=Za−Zb

知道三个坐标轴方向上的差值后再用勾股定理就可以求出两点间距离了，即：
$L=\sqrt{\Delta X^2+\Delta Y^2+\Delta Z^2}$L=ΔX2+ΔY2+ΔZ2​
这里说明一下，海拔高度H可有可无，如果有的话，注意H与R单位要统一。普通GPS接收机给出的海拔一般很不准确，所以不推荐使用。另外NMEA规范报文中有两个量涉及到海拔，注意计算。

（注：这里求算的L其实可以看成为弦长，求取弧长只需再结合R用反三角函数即可求得对应的弧长，但是这样一来感觉有点“画蛇添足”了，如果这么求弧长倒不如直接用前面的两种方法了。）

二、航向的求算

方法1、球面正弦公式法

适用范围：理论上，这个公式可以用于地球上任意两点间航向的求算，但是，这个方法求出的角度在“后处理”上存在缺陷（关于缺陷的原因及解决方法会在后面说明），而且因为使用了球面正弦公式的余弦值，同样对系统浮点运算精度有较高要求，因此不推荐使用此方法。如果要使用，则这个方法只能在短距离内使用，低纬度地区建议300km以下，中纬度地区建议100km以下，高纬度地区建议40km以下。

已知：$Aj，Aw，Bj，Bw$Aj，Aw，Bj，Bw

求解：

在“距离的求算”的“方法1”中求得了角c的余弦值，要求得它的正弦值，所用的公式就是三角函数里最基本正弦余弦转换函数的一个变形

$sin(c)=\sqrt{1-cos^2(c)}$sin(c)=1−cos2(c)​

求得正弦后，接下来我们要用一个不太常用的公式，球面正弦公式

$\cfrac{sin(a)}{sin(A)}=\cfrac{sin(b)}{sin(B)}=\cfrac{sin(c)}{sin(C)}$sin(A)sin(a)​=sin(B)sin(b)​=sin(C)sin(c)​

将已知数据代入并稍微变形一下，公式写为：

$sin(A)=\cfrac {sin(90-Bw)*sin(Bj-Aj)}{sin(c)}$sin(A)=sin(c)sin(90−Bw)∗sin(Bj−Aj)​

用反正弦函数求角度，于是上式就写成

$A=arcsin(\cfrac {sin(90-Bw)*sin(Bj-Aj)}{sin(c)})$A=arcsin(sin(c)sin(90−Bw)∗sin(Bj−Aj)​)

这里需要注意一点，我们一开始的假设便是求B点相对于A点的航向，因此这里是Bj-Aj，不要写反，否则后面得不到正确结果。

算到这里，还没有完，得到的结果并不总符合我们对航向的定义，因此要根据B相对于A的位置在四个象限两个轴上进行讨论，依据不同情况对计算结果进行不同处理。假设A点固定于原点，则:

$B点在第一象限，Bearing=A；$B点在第一象限，Bearing=A；

$B在第二象限，Bearing=360+A;$B在第二象限，Bearing=360+A;

$B在第三四象限，Bearing=180-A。$B在第三四象限，Bearing=180−A。

这里只说了象限的讨论结果，因为轴上的讨论更复杂些，要结合程序运行环境一起考虑，考虑的主要因素是系统的计算精度。譬如，在三面角余弦公式中，当AB点纬度值相同时，对公式的值起决定作用的就是cos(Bj-Aj)这一项，当Bj-Aj的值比较小时，例如0.0001（这在赤道地区对应的长度为11米左右），用一般的计算器计算时值为1，这样，后面的计算便不可能完成。但是，如果用计算机计算则为0.999999999998476913…………。所以，基于以上原因，需要对轴的“范围进项扩充”，要用单片机、手机运算的尤其要注意。

经过一系列计算，最后，就得到了最终结果。

---

到这里，上面是我最开始写的一个方法，还对最后结果进行了分情况讨论，似乎没什么不妥，其实就是这一段分象限讨论使这个方法不再完美，因为对一个极坐标下的结果用直角坐标系来对它讨论就是错误。依旧举个栗子：

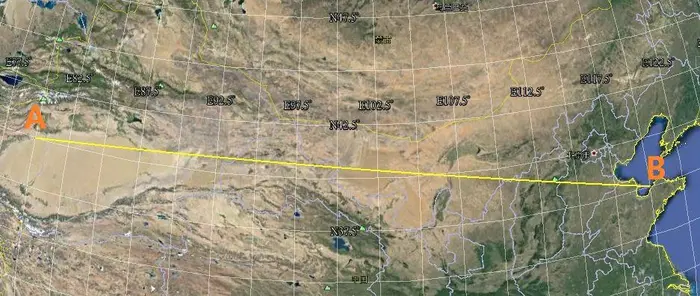
（白色线为经纬线，黄色线为AB最短路径）

$A点经纬度：40°N，80°E。B点经纬度：37.55°N，120°E。$A点经纬度：40°N，80°E。B点经纬度：37.55°N，120°E。

按照上面的方法，B点应该在第四象限，也就是航向应当为98.53°，但是实际上在A点向B点走，要先朝81.4651°的方向走，因此，可以说，上面的象限讨论完全就是个错误（虽然这个错误在短距离内与实际值偏差微乎其微），对轴的范围进行扩充跟加剧了这个错误。目前，可以使用“距离的求算”中“Haversine法”的反正弦结果进行稍微处理以代替球面余弦公式所得的余弦结果，从而省去对轴的扩充，但是到目前，我还没有找到一个将上述结果转化成符合航向定义的合理方法。

方法2、平面直角坐标系法

适用范围：这个方法我的基本思路就是将经度差和纬度差转化成地面距离再运用平面几何知识求解，所以只能用于短距离求算，中纬度地区建议40km以下。因为计算更简便，所以相对来说有优势。

已知：$Aj，Aw，Bj，Bw$Aj，Aw，Bj，Bw

求解：

$A=arcsin(\cfrac {(Bj-Aj)*cos(Bw)}{Bw-Aw})$A=arcsin(Bw−Aw(Bj−Aj)∗cos(Bw)​)
当

$B点在第一象限及Y轴正半轴，Bearing=A；$B点在第一象限及Y轴正半轴，Bearing=A；

$B在第二象限，Bearing=360+A；$B在第二象限，Bearing=360+A；

$B在第三四象限及Y轴负半轴，Bearing=180+A。$B在第三四象限及Y轴负半轴，Bearing=180+A。

对于某些系统，再单独设定B位于X正负半轴上的值就可以了，有些系统可以返回$arctan（X/0）=90。$arctan（X/0）=90。

三、第二点经纬度的求算

适用范围：这个方法其实就是“航向的求算”“球面正弦公式法”的再次运用。目前未发现有任何限制，因为这当中没有象限讨论，因此不会发生两种坐标系冲突的低级错误。

已知：$Aj，Aw，L，R，Bearing$Aj，Aw，L，R，Bearing

求解：

首先求算c，

$rad(c)=\frac{L}{R}$rad(c)=RL​
$c=rad(c)*\cfrac{180}{\pi}$c=rad(c)∗π180​
（注意此处L、R的单位要统一）
之后求解a，将已知量代入，公式为：

$a=arccos(cos(90-Aw)*cos(c)+sin(90-Aw)*sin(c)*cos(Bearing))$a=arccos(cos(90−Aw)∗cos(c)+sin(90−Aw)∗sin(c)∗cos(Bearing))

求得a之后我们求解C，

$c=arcsin(\cfrac{sin(c)*sin(Bearing)}{sin(a)})$c=arcsin(sin(a)sin(c)∗sin(Bearing)​)

写到这里应该都恍然大悟了吧，

$Bw=90-a$Bw=90−a

$Bj=Aj+C$Bj=Aj+C

PS：对于上面两个三角公式的理解，可以想成把A点作为北极点。

主要介绍就到这里，我们在做具体的项目时关键就是几个公式的利用！知其然也知其所以然是最好的！