一、因子分解机FM的模型
因子分解机(Factorization Machine, FM)是由Steffen
Rendle提出的一种基于矩阵分解的机器学习算法。
1、因子分解机FM的优势
对于因子分解机FM来说,最大的特点是对于稀疏的数据具有很好的学习能力。现实中稀疏的数据很多,例如作者所举的推荐系统的例子便是一个很直观的具有稀疏特点的例子。
2、因子分解机FM的模型
对于度为2的因子分解机FM的模型为:
其中,参数 ,
, ,
, 。
。 表示的是两个大小为
表示的是两个大小为 的向量
的向量 和向量
和向量 的点积:
的点积:
其中, 表示的是系数矩阵
表示的是系数矩阵 的第
的第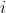 维向量,且
维向量,且 ,
, 称为超参数。在因子分解机FM模型中,前面两部分是传统的线性模型,最后一部分将两个互异特征分量之间的相互关系考虑进来。
称为超参数。在因子分解机FM模型中,前面两部分是传统的线性模型,最后一部分将两个互异特征分量之间的相互关系考虑进来。
因子分解机FM也可以推广到高阶的形式,即将更多互异特征分量之间的相互关系考虑进来。
二、因子分解机FM算法
因子分解机FM算法可以处理如下三类问题:
-
回归问题(Regression)
-
二分类问题(Binary Classification)
-
排序(Ranking)
在这里主要介绍回归问题和二分类问题。
1、回归问题(Regression)
在回归问题中,直接使用 作为最终的预测结果。在回归问题中使用最小均方误差(the
least square error)作为优化的标准,即
作为最终的预测结果。在回归问题中使用最小均方误差(the
least square error)作为优化的标准,即
其中,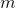 表示样本的个数。
表示样本的个数。
2、二分类问题(Binary Classification)
与Logistic回归类似,通过阶跃函数,如Sigmoid函数,将 映射成不同的类别。在二分类问题中使用logit
loss作为优化的标准,即
映射成不同的类别。在二分类问题中使用logit
loss作为优化的标准,即
其中, 表示的是阶跃函数Sigmoid。具体形式为:
表示的是阶跃函数Sigmoid。具体形式为:
三、因子分解机FM算法的求解过程
1、交叉项系数
在基本线性回归模型的基础上引入交叉项,如下:
若是这种直接在交叉项 的前面加上交叉项系数
的前面加上交叉项系数 的方式在稀疏数据的情况下存在一个很大的缺陷,即在对于观察样本中未出现交互的特征分量,不能对相应的参数进行估计。
的方式在稀疏数据的情况下存在一个很大的缺陷,即在对于观察样本中未出现交互的特征分量,不能对相应的参数进行估计。
对每一个特征分量 引入辅助向量
引入辅助向量 ,利用
,利用 对交叉项的系数
对交叉项的系数 进行估计,即
进行估计,即
令
则
这就对应了一种矩阵的分解。对 值的限定,对FM的表达能力有一定的影响。
值的限定,对FM的表达能力有一定的影响。
2、模型的求解
这里要求出 ,主要采用了如公式
,主要采用了如公式 求出交叉项。具体过程如下:
求出交叉项。具体过程如下:
3、基于随机梯度的方式求解
对于回归问题:
对于二分类问题:
而
四、实验(求解二分类问题)
1、实验的代码:
-
#coding:UTF-8
-
-
from __future__ import division
-
from math import exp
-
from numpy import *
-
from random import normalvariate#正态分布
-
from datetime import datetime
-
-
trainData = 'E://data//diabetes_train.txt'
-
testData = 'E://data//diabetes_test.txt'
-
featureNum = 8
-
-
def loadDataSet(data):
-
dataMat = []
-
labelMat = []
-
-
fr = open(data)#打开文件
-
-
for line in fr.readlines():
-
currLine = line.strip().split()
-
#lineArr = [1.0]
-
lineArr = []
-
-
for i in xrange(featureNum):
-
lineArr.append(float(currLine[i + 1]))
-
dataMat.append(lineArr)
-
-
labelMat.append(float(currLine[0]) * 2 - 1)
-
return dataMat, labelMat
-
-
def sigmoid(inx):
-
return 1.0 / (1 + exp(-inx))
-
-
def stocGradAscent(dataMatrix, classLabels, k, iter):
-
#dataMatrix用的是mat, classLabels是列表
-
m, n = shape(dataMatrix)
-
alpha = 0.01
-
#初始化参数
-
w = zeros((n, 1))#其中n是特征的个数
-
w_0 = 0.
-
v = normalvariate(0, 0.2) * ones((n, k))
-
-
for it in xrange(iter):
-
print it
-
for x in xrange(m):#随机优化,对每一个样本而言的
-
inter_1 = dataMatrix[x] * v
-
inter_2 = multiply(dataMatrix[x], dataMatrix[x]) * multiply(v, v)#multiply对应元素相乘
-
#完成交叉项
-
interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2.
-
-
p = w_0 + dataMatrix[x] * w + interaction#计算预测的输出
-
-
loss = sigmoid(classLabels[x] * p[0, 0]) - 1
-
print loss
-
-
w_0 = w_0 - alpha * loss * classLabels[x]
-
-
for i in xrange(n):
-
if dataMatrix[x, i] != 0:
-
w[i, 0] = w[i, 0] - alpha * loss * classLabels[x] * dataMatrix[x, i]
-
for j in xrange(k):
-
v[i, j] = v[i, j] - alpha * loss * classLabels[x] * (dataMatrix[x, i] * inter_1[0, j] - v[i, j] * dataMatrix[x, i] * dataMatrix[x, i])
-
-
-
return w_0, w, v
-
-
def getAccuracy(dataMatrix, classLabels, w_0, w, v):
-
m, n = shape(dataMatrix)
-
allItem = 0
-
error = 0
-
result = []
-
for x in xrange(m):
-
allItem += 1
-
inter_1 = dataMatrix[x] * v
-
inter_2 = multiply(dataMatrix[x], dataMatrix[x]) * multiply(v, v)#multiply对应元素相乘
-
#完成交叉项
-
interaction = sum(multiply(inter_1, inter_1) - inter_2) / 2.
-
p = w_0 + dataMatrix[x] * w + interaction#计算预测的输出
-
-
pre = sigmoid(p[0, 0])
-
-
result.append(pre)
-
-
if pre < 0.5 and classLabels[x] == 1.0:
-
error += 1
-
elif pre >= 0.5 and classLabels[x] == -1.0:
-
error += 1
-
else:
-
continue
-
-
-
print result
-
-
return float(error) / allItem
-
-
-
if __name__ == '__main__':
-
dataTrain, labelTrain = loadDataSet(trainData)
-
dataTest, labelTest = loadDataSet(testData)
-
date_startTrain = datetime.now()
-
print "开始训练"
-
w_0, w, v = stocGradAscent(mat(dataTrain), labelTrain, 20, 200)
-
print "训练准确性为:%f" % (1 - getAccuracy(mat(dataTrain), labelTrain, w_0, w, v))
-
date_endTrain = datetime.now()
-
print "训练时间为:%s" % (date_endTrain - date_startTrain)
-
print "开始测试"
-
print "测试准确性为:%f" % (1 - getAccuracy(mat(dataTest), labelTest, w_0, w, v))
2、实验结果:

五、几点疑问
在传统的非稀疏数据集上,有时效果并不是很好。在实验中,我有一点处理,即在求解Sigmoid函数的过程中,在有的数据集上使用了带阈值的求法:
-
def sigmoid(inx):
-
#return 1.0 / (1 + exp(-inx))
-
return 1. / (1. + exp(-max(min(inx, 15.), -15.)))
欢迎更多的朋友一起讨论这个算法。
参考文章
1、Rendle, Factorization Machines.
2、Factorization Machines with libFM
 ,
, ,
, 。
。 表示的是两个大小为
表示的是两个大小为 的向量
的向量 和向量
和向量 的点积:
的点积:
 表示的是系数矩阵
表示的是系数矩阵 的第
的第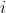 维向量,且
维向量,且 ,
, 称为超参数。在因子分解机FM模型中,前面两部分是传统的线性模型,最后一部分将两个互异特征分量之间的相互关系考虑进来。
称为超参数。在因子分解机FM模型中,前面两部分是传统的线性模型,最后一部分将两个互异特征分量之间的相互关系考虑进来。
 作为最终的预测结果。在回归问题中使用最小均方误差(the
least square error)作为优化的标准,即
作为最终的预测结果。在回归问题中使用最小均方误差(the
least square error)作为优化的标准,即
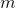 表示样本的个数。
表示样本的个数。
 映射成不同的类别。在二分类问题中使用logit
loss作为优化的标准,即
映射成不同的类别。在二分类问题中使用logit
loss作为优化的标准,即
 表示的是阶跃函数Sigmoid。具体形式为:
表示的是阶跃函数Sigmoid。具体形式为:
 的前面加上交叉项系数
的前面加上交叉项系数 的方式在稀疏数据的情况下存在一个很大的缺陷,即在对于观察样本中未出现交互的特征分量,不能对相应的参数进行估计。
的方式在稀疏数据的情况下存在一个很大的缺陷,即在对于观察样本中未出现交互的特征分量,不能对相应的参数进行估计。
 引入辅助向量
引入辅助向量 ,利用
,利用 对交叉项的系数
对交叉项的系数 进行估计,即
进行估计,即
 值的限定,对FM的表达能力有一定的影响。
值的限定,对FM的表达能力有一定的影响。
 ,主要采用了如公式
,主要采用了如公式 求出交叉项。具体过程如下:
求出交叉项。具体过程如下:
