分类问题

首先了解二分类问题：例如垃圾邮件分类，肿瘤良性恶性问题等等，即

此类问题不适合用线性回归来做，下面我们了解一种新的算法：Logistic Regression（逻辑回归算法，首先它既不是逻辑也不是回归），逻辑回归算法的输出值在0到1之间。

逻辑回归算法

假设函数设置为一个S型函数（也可以叫逻辑函数），其输出值在（0，1）。假设函数的输出值可以理解为对新输入样本x的y=1或者y=0的概率的估计值，也就是在给定x和的条件下y=1或者y=0的概率，或者，同时。这里怎么理解假设函数会将y预测为哪种呢？只要该假设函数，则预测y=1的概率，反之，则预测y=0的概率。

首先了解假设函数的一个重要属性：决策边界

将整个平面分成了两部分，一片为y=1的区域，另一片为y=0的区域，线性非线性情况下都是如此，和多项式回归类似，对于非线性情况我们可以通过增加高阶多项式来拟合数据，以至于得到的决策边界会是些奇奇怪怪的形状，需要注意的是不是用训练集来定义决策边界，而是用训练集来拟合参数。

逻辑回归模型的拟合问题

我们如何拟合这个参数呢？

首先从线性回归的方法中试试看

这里代价函数与线性回归时使用的代价函数做小小的改动：

定义一个代价值Cost函数：，方便起见，去掉了和得上标

如果我们可以最小化Cost函数，便能使得代价函数值最小

但是很容易可以看出是非线性的，代入到中得到的图像将会是个非凸函数，具有很多局部最小值，这种情况下使用梯度下降法就很有可能无法找到全局最小值，所以我们需要改变代价函数。

下面这个就是逻辑回归所用的代价函数中的代价值Cost函数：

分类问题的输出值为（0，1），这个Cost函数就很适合

如果y = 1, =1, 则Cost = 0；如果  0，则Cost ∞

如果y = 0, =0, 则Cost = 0；如果  1，则Cost ∞

这里为什么用log函数，我想可能是因为log就是ln，方便后面对代价函数求偏导。

但是Cost写成两行很别扭，这里我们把它转成一行：

（这个应该不难理解吧）

得到最终的代价函数：

采用梯度下降法找出最小化的: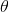

即，推导过程和线性回归算法中的类似，但是假设函数和线性回归中的完全不同，所以逻辑回归中的梯度下降与线性回归中的梯度下降是两个东西。

PS：除了梯度下降法最小化代价函数之外，还有更高级的算法：共轭梯度法、BFGS(变尺度法)、L-BFGS(限制变尺度法)等等，这些算法有很多有点：1、不需要手动选择学习率，它们内部有一个线性搜索算法能自动的尝试不同的；2、收敛速度远远快于梯度下降。缺点就是太复杂(大佬都花了好几年才理解透其中的细节)。

多分类问题

解决多分类问题的思路是把多分类转为二分类问题，实现n个二分类器，这个应该不难理解：