神经网络总结

step1:选择神经网络架构

确定输入单元数（一般与训练集特征数相符）、输出单元数、以及隐藏层。如果隐藏层大于1层，那么所有的隐藏层的单元数应该相等。

如图：输出单元为3，输出单元为4，隐藏层单元数为5。如果训练集（x,y),y有四个值{1，2，3，4}那么需要用向量来表示如4可以表示为

step2:初始化权重

在逻辑回归或者线性回归问题中，我们使用梯度下降方法时，初始化为0.这样一般没什么问题，但是在神经网络中，我们不可以初始化为0，因为这样在每一次更新中，从输入单元到隐藏层单元的参数一直都是相等的。（需要再次梳理）这样会导致神经网络失效。因此我们需要使用随机函数rand()来初始化.我们将放在一个小的区间里。

其中，rand(10，11）是生成一个10*11的矩阵，其中矩阵里面的值位于0~1之间。INIT_EPSILON是自定义的一个值，如上处理之后就让theta位于了。

step3:实现前向传播，求得所有x对应的h

分析：为输入层，按照如上计算，就算出第四层也是最终的h（怎么知道每个x对应的h??)

step4:求解代价函数J

与逻辑回归相比，由于神经网络输出单元可能不止一个因此需要使用一层来求解每个单元的输出。除此之外，正规化惩罚项部分：由此存在多个以及上节提及的定义：：表示的是第L层第j个单元到第L+1第j+1个单元的权重。因此我需要使用两次求和符号，两层之间一共需要求解个，然后再从层数进行求和。

step5:使用后向传播方法求解J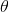（）的偏导数：

首先定义:第L层第j个单元的误差。

例：

注意:没有,因此输入层x输入的是真实的数据，不存在误差。（不清楚这些推导）

Step6:梯度检查，确认后向传播中没有出现bug

用双侧查分来检查：

如果双侧差分的结果和后向传播的结果相近，那么认为没有出现bug,则可以使用这个偏导。此时，记得关闭或者禁用梯度检查，以免拖慢速度影响效率。

step7:使用梯度下降或者其他方法对J进行最小化，得到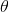

这里使用的偏导是通过后向传播得到的那个偏导。