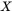您的位置: 首页  >  文章  >  马尔可夫链与“熵”的结合（初稿）

马尔可夫链与“熵”的结合（初稿）

分类: 文章 • 2025-07-04 15:04:34
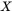针对随机变量 马尔可夫链与“熵”的结合（初稿）X ，其熵 马尔可夫链与“熵”的结合（初稿）H(X)=-\sum_x p(x)\log_2 p(x) 可以衡量 马尔可夫链与“熵”的结合（初稿）X 的不确定度。
复杂一点，联合分布 马尔可夫链与“熵”的结合（初稿）(X,Y) ，熵为 马尔可夫链与“熵”的结合（初稿）H(X,Y)=-\sum_x\sum_yp(x,y)\log_2p(x,y) 。
而当这里的随机变量 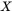马尔可夫链与“熵”的结合（初稿）X 变成一个随机过程 马尔可夫链与“熵”的结合（初稿）\{X_i\} 时，就有必要重新思考如何度量不确定度了。单个的定义 马尔可夫链与“熵”的结合（初稿）H(X_i) 不是很好，于是我们干脆定义一个比较平均一点的熵-熵率。
Definition 1：熵率（entropy rate）：若极限 马尔可夫链与“熵”的结合（初稿）H(\chi)=\lim_{n \rightarrow \infty}\frac{{H(X_1,X_2,...,X_n)}}{n}存在，则马尔可夫链与“熵”的结合（初稿）H(\chi)称为马尔可夫链与“熵”的结合（初稿）{X_i}的熵率
另一个量也与熵率有不可描述的联系： 马尔可夫链与“熵”的结合（初稿）\qquad \quad H(\chi')=\lim_{n\rightarrow\infty}H(X_n|X_{n-1},X_{n-2},...,X_1)
这两个量也不过是反映一个随机过程的entropy怎么变化的。
而以此定义的同时，会得到一个比较漂亮的结果，如下：
Theorem 1：一个平稳随机过程 马尔可夫链与“熵”的结合（初稿）\{X_i\} （ 即马尔可夫链与“熵”的结合（初稿）P(X_1=x_1,X_2=x_2,....,X_n=x_n) = P(X_{1+l},X_{2+l},...,X_{n+l}) ，任意连续n个状态之间的联系和时间无关），它的 马尔可夫链与“熵”的结合（初稿）H(\chi)=H(\chi')
这个证明其实比较容易，淑芬中有一道经典的习题 马尔可夫链与“熵”的结合（初稿）\qquad 已知\lim_ { n \rightarrow \infty}a_n=a,那么\lim_{n\rightarrow \infty}\frac{\sum_{i=0}^na_i}{n} = a
这道题在这里有了运用。
马尔可夫链与“熵”的结合（初稿）H(X_n|X_{n-1},...,X_1)=H(X_{n+1}|X_n,...,X_2) \\ \geq H(X_{n+1}|X_n,...,X_2,X_1)
第一个等式是平稳性得到，后面相当于说明了马尔可夫链与“熵”的结合（初稿）a_n 是递减恒正， 则马尔可夫链与“熵”的结合（初稿）a_n 自然有极限，
结合马尔可夫链与“熵”的结合（初稿）\frac{H(X_1,..,X_n)}{n}=\frac{1}{n}\sum_{i=1}^nH(X_i|X_{i-1},...,X_1)\\
两边取极限，可以很容易得证

而这个漂亮的性质，应用在我们的马尔科夫过程中，就有更加亦可赛艇的结论！
先上马尔可夫过程（又称为马尔可夫链）定义
Definition 2：马尔可夫链(Markov chain or Markov process)离散随机过程 马尔可夫链与“熵”的结合（初稿）\{X_i\} 满足 马尔可夫链与“熵”的结合（初稿）P(X_n=x_n|X_{n-1}=x_{n-1},...,X_1=x_1) = P(X_n=x_n|X_{n-1}=x_{n-1}) 则称其为马尔可夫链
对于这个定义，其实有一个比较有趣的概括
Knowing the present state, the future of the system is independent of the past.
某种程度上相当于：对于现在的你来说，未来永远与过去无关 （这句话...或许能拿来煲一碗鸡汤）
那么这样来的话，对于平稳的Markov chain，初始为平稳分布，它的熵率马尔可夫链与“熵”的结合（初稿）H(\chi) = \lim_{n\rightarrow \infty}H(X_n|X_{n-1}) = H(X_2|X_1) \\ =-\sum_{x_1,x_2}p(x_1)p(x_2|x_1)\log_2 p(x_2|x_1)
马尔可夫链与“熵”的结合（初稿）

所以对于Markov chain求熵率其实很简单，然而我们眉头微微一皱，会发现事情并不简单。经常会有随机过程不是Markov chain，而是Markov chain的函数
比如离散的随机过程 马尔可夫链与“熵”的结合（初稿）\{Y_i\} 和平稳的Markov chain 马尔可夫链与“熵”的结合（初稿）\{X_i\} 满足 马尔可夫链与“熵”的结合（初稿）Y_i=f(X_i) 。
其实问题并不复杂.....
重新思考下可以发现：

显然这个随机过程是平稳的，因此也可以用 马尔可夫链与“熵”的结合（初稿）H(Y_n|Y_{n-1},...,Y_1)\rightarrow H(\Upsilon) 来求熵率，但除此之外我们有一些奇妙的结论，比如关于马尔可夫链与“熵”的结合（初稿）\{Y_i\} 的夹逼不等式。
Theorem 2： 马尔可夫链与“熵”的结合（初稿）H(Y_n|Y_{n-1},...,Y_1,X_1)\leq H(\Upsilon) \leq H(Y_n|Y_{n-1},...,Y_1) 且 马尔可夫链与“熵”的结合（初稿）\lim_{n\rightarrow\infty}H(Y_n|Y_{n-1},...,Y_1,X_1)= H(\Upsilon) = \lim_{n\rightarrow\infty}H(Y_n|Y_{n-1},...,Y_1)
定理的证明有点巧，但也自然，两个式子的右式的证明，在前面说明 马尔可夫链与“熵”的结合（初稿）\qquad H(Y_n|Y_{n-1},...,Y_1)\quad关于n递减,取极限时给过了。问题主要是左边的式子的证 明。
对于第一个不等式来说，我们想办法把Markov chain的性质和平稳的性质用上去。 马尔可夫链与“熵”的结合（初稿）\begin{align} H(Y_n|Y_{n-1},...,Y_1,X_1) &\leq H(Y_n|Y_{n-1},...,Y_1,X_1,_...,X_{-k})\qquad Markov \quad chain性质 \\ &=H(Y_n|Y_{n-1},...,Y_1,X_1,_...,X_{-k},Y_{-k},..Y_{1}) \quad 因为Y_i是X_i的函数\\ &= H(Y_{n+k}|Y_{n+k-1},.....,Y_1,X_k,...,X_1)\quad平稳性质\\ &\leq H(Y_{n+k}|Y_{n+k-1},...,Y_{1}) \end{align}
再令 马尔可夫链与“熵”的结合（初稿）k\rightarrow \infty 得证
第二个等式来说仿照上面的证法，利用马尔可夫链与“熵”的结合（初稿）H(Y_n|Y_{n-1},...,Y_1,X_1)-H(Y_n|Y_{n-1},...,Y_1)=I(X_1;Y_n|Y_{n-1},...,Y_1)\\ 和 马尔可夫链与“熵”的结合（初稿）\sum_{n=1}^{\infty}I(X_1;Y_n|Y_{n-1},...,Y_1)=\lim_{n{\rightarrow}\infty}I(X_1;Y_1,...,Y_n) 就能得证

于是乎，这篇文章讲了什么呢？
emmm......主要讲了怎么定义随机过程的“熵”以及怎么求这个“熵”，尤其是Markov chain的熵率，大概就是这样。

相关推荐