支持向量机——SVM简介

简介

支持向量机（support vector machines，SVM）是一种二分类模型，分类学习最基本的想法就是基于训练集D在样本空间中找到一个划分超平面。但是能将训练样本分开的划分超平面可能有很多，我们的目的就是找到两类训练样本“正中间”的划分超平面。其学习策略是使间隔最大化，最终转换为一个凸二次规划问题的求解。

支持向量机——SVM简介

理论基础

超平面

超平面是由三维空间中的平面向高维推广的概念，其本质是自由度比空间维度小1的“平面”。自由度可以理解为超平面方程的自由变量，例如三维空间中，对于平面 $Ax+By+Cz+D=0$ （A、B、C、D已知），当x、y确定时z唯一确定，即x、y为自由变量，自由度为2。

在样本空间中，超平面用如下线性方程来表示： $w^Tx+b=0$ ，其中 $\omega$ 是超平面的法向量， $b$ 为位移项。

线性可分性

给定一个数据集，如果存在超平面能将正实例点和负实例完全划分到超平面的两侧，则为线性可分；否则线性不可分。

线性可分模型举例：

支持向量机——SVM简介

线性不可分模型举例：

支持向量机——SVM简介

感知机模型

感知机学习旨在求出将训练数据进行线性划分的分离超平面，为此，导入基于误分类的损失函数，利用梯度下降法对损失函数进行极小化，求得感知机模型。输入特征向量，输出为实例的类别。

输入空间到输出空间对应如下函数：

$f(x)=\begin{cases}1& \text{w*x+b>=0}\\-1& \text{w*x+b<0}\end{cases}$

这里很容易看出误分类数据满足 $y_i*(wx_i+b)<0$ 。所以误分类点到超平面S的总距离为： $-\frac 1 {||w||}\Sigma y_i*(wx_i+b)$

我们可以确定损失函数为： $L(w,b)=-\Sigma y_i*(wx_i+b)$ 。（ $||w||$ 为定值）

在梯度下降极小化损失函数的过程中，随机选取一个误分类点，更新 $w、b$ ，并迭代直到没有误分类点。损失函数的梯度：

支持向量机——SVM简介

$w、b$ 的更新：

支持向量机——SVM简介

需要注意的是当训练集线性不可分的时候，感知机不收敛，迭代结果会发生震荡，这时需要用到核函数。

间隔

首先给出几何间隔表达式：

$\gamma^{(i)}=y^{(i)}*\frac{(w^Tx+b)}{||w||}$

其中 $||w||$ 是 $w$ 的L2范数（即欧式距离）。

注意区别函数间隔。

和感知机模型类似，对一个数据点进行分类，当超平面离数据点的“间隔”越大，分类的确信度也越大。所以，为了使得分类的确信度尽量高，需要让所选择的超平面能够最大化这个“间隔”值。最优的超平面就是最大间隔超平面。

支持向量机——SVM简介

支持向量

样本空间中距离超平面最近的一个或多个点。如上图中的实心红点和空心红点。

最优化问题

那么如何求出最大间隔超平面？

首先我们需要求出两类样本到超平面间隔的最小值，相加后使间距和最大。即使得两端距离超平面最近的样本点到超平面的距离和最大。

取 $r=min\ r_i$ ，所以支持向量到超平面的距离为r，其他点到超平面的距离大于r。于是有：

$\begin{cases} \frac{w^Tx+b}{||w||}>=r &\text{y=+1} \\\frac{w^Tx+b}{||w||}<=-r &\text{y=-1} \end{cases}$

令 $||w||*r=1$ ，有

$\begin{cases} w^Tx+b>=1 &\text{y=+1} \\w^Tx+b<=-1 &\text{y=-1} \end{cases}$

这里是因为w和b可以等比例扩大而超平面不变，无论r是多少，我们都可以对w和b进行相应的变换，使 $||w||*r=1$ 。此时 $r=\frac 1{||w||}$ 。

将两个方程合并之后可以得到：

$y(w^Tx+b)>=1$

要使异类支持向量到超平面的距离和最大，即

$max_{w,b}\ \frac 2{||w||}\ \ \ \ s.t.\ y_i(w^Tx_i+b) \geq 1$

稍微变化一下，约束条件就是 $min_{w,b}\ \frac 12||w||^2$ 。

拉格朗日数乘法

基本思想：引入拉格朗日乘子，将含有n个变量k个约束条件的约束优化问题转换为含有n+k个变量的无约束优化问题，即把条件极值转换为无条件极值。这里不赘述。

凸二次规划问题

目标函数为二次的，约束条件是线性的。

凸优化：大意就是在以凸集为定义域的凸函数上找到最小值点。

KKT条件

一般地，一个最优化数学模型能够表示成下列标准形式：

支持向量机——SVM简介

KKT条件就是指上面最优化数学模型的标准形式中的最小点 x* 必须满足下面的条件：

支持向量机——SVM简介

对偶问题

引入对偶问题的优点在于：一方面对偶问题往往更容易求解；另一方面可以自然地引入核函数，向非线性分类推广。

将上述的优化问题引入拉格朗日乘子，即

$L(w ,b, \alpha)=\frac 12||w||^2+\Sigma ^m_{i=1}\alpha_i(1-y_i(w^Tx_i+b))$

然后令 $\theta(w)=max_{a_i\geq 0}L(w,b,\alpha)$ ，有

$\theta(w)=\begin{cases} \frac {1}{2} ||w||^2 &\text{yi(wT*xi+b)>=1} \\ \infty &\text{yi(wT*xi+b)<1} \end{cases}$

从而目标函数由 $min_{w,b}\ \frac 12||w||^2$ 变成了 $min_{w,b}\theta(w)=min_{w,b}max_{\alpha_i\geq0}L(w,b,\alpha)=p^*$ 。

可以交换max和min的位置转换成对偶问题 $max_{\alpha_i\geq0}min_{w,b}L(w,b,\alpha)=d^*$ ，这里 $d^*是p^*$ 的近似解，且在满足KKT条件时两者等价。

求解此对偶问题，可以划分为三个步骤：一、 $min_{w、b}$ ；二、 $\alpha$ 的极小；三、SOM算法

一、 $min_{w,b}$

分别对w、b求偏导：

支持向量机——SVM简介

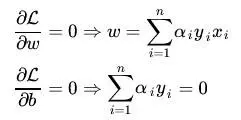
将对w求偏导的式子带回函数 $L(w,b,\alpha)$ 中：（具体过程参考西瓜书）

支持向量机——SVM简介

结果：消去了 $w,b$ ，将拉格朗日方程转换为只包含一个变量即 $\alpha$ 的形式。

二、 $\alpha$ 的极小

步骤一将对偶问题转换为

支持向量机——SVM简介

从而求出 $\alpha_i$ 。

三、SMO算法

每次选出两个分量 $a_i,a_j$ 进行调整，其他分量保持不变，在得到解后，再用其改变其他分量。

核函数

上述讨论均建立在训练样本线性可分的条件上。当问题不是线性可分的的时候，通过引入核函数k(·,·）可以将样本空间映射到一个更高维的特征空间，并使样本在该空间内线性可分。

在线性不可分的情况下，SVM首先在低位空间中完成计算，然后通过核函数将输入空间映射到高维特征空间，最终在高维特征空间中构造出最优分离超平面。

例如，对于上面二维的线性不可分问题，一个明显的分界应该是一个圆圈，二不能用直线（二维中的超平面）划分，用于分界的圆圈在二维空间中可以表示为：

$a_1X_1+a_2X_2+a_3X_1X_2+a_4X_1^2+a_5X_2^2+a_6=0$

通过 $Z_1=X_1X_2,Z_2=X_1^2,Z_3=X_2^2,Z_4=X_1,Z_5=X_2$ 变换，将二维投射到五维空间，就可以将问题转换为线性问题。

相当于把问题：

支持向量机——SVM简介

中的 $x_i->\phi(x_i), x_j->\phi(x_j)$ 。

这个方法虽然简便，但是低维到高维的数目是爆炸增长的。二维映射到五维，三维映射到十九维，等等，这在计算时是难以接受的。

我们比较映射后的内积 $<\phi(x_1),\phi(x_2)>$ 和 $(<x_1,x_2>+1)^2$ 可以发现，展开后的结果是极为相似的，只需加上常数项，并将某几个维度线性放缩，就可以相互转换。

这种将两个向量隐式映射到高维空间中的函数叫核函数。即 $k(x_1,x_2)=(<x_1,x_2>+1)^2$ 。用这种方法就可以将分类函数和对偶问题中的内积隐式映射到高维，而避免在高维中的计算。

松弛变量

在线性不可分的一些问题里，有时候将数据映射到高维空间后，仍然不好处理，或是数据本身有噪点。这时引入松弛变量，将约束条件变为：

$y_i(w^Tx_i+b)\geq 1-\xi_i$

其中 $\xi_i\geq 0$ 称为松弛变量，从而允许两个临界超平面内存在点。当然此时目标函数也要相应改变。

参考资料：

支持向量机通俗导论（理解SVM的三层境界）

西瓜书

机器学习感知机（统计学习-李航）

支持向量机（SVM）——原理篇

支持向量机——SVM简介

简介

理论基础

相关推荐