凸优化学习（二）对偶和SVM

4.4 对偶问题

对于有约束的优化问题。约束优化问题的一般形式为：

拉格朗日函数

合并目标函数与约束条件。

L(x,λ,v)=f0(x)+∑mi=1λifi(x)+∑pi=1vihi(x)$L(x,\lambda ,v)=f_0(x)+\sum _{i=1}^m{\lambda }_i{f}_i(x)+\sum _{i=1}^p{v}_i{h}_i(x)$

其中，主变量为x，对偶变量为λ≥0,v$\lambda \ge \mathbb{0}\mathbb{,}\mathbb{v}$

经过这种定义，一般约束问题转换为以下主问题：

p∗=minx(maxλ,vL(x,λ,v))$p^{\ast }=mi{n}_x(ma{x}_{\lambda ,v}L(x,\lambda ,v))$

因为，maxλ,vL(x,λ,v)=f0(x)+maxλ,v(λTf(x)+vTh(x))$ma{x}_{\lambda ,v}L(x,\lambda ,v)=f_0(x)+ma{x}_{\lambda ,v}({\lambda }^{T}f(x)+v^{T}h(x))$ ，

• 当x在可行域内时，vTh(x)=0$v^{T}h(x)=0$ ，λTf(x)≤0${\lambda }^{T}f(x)\le 0$ 的最大值为0，因此上式maxλ,vL(x,λ,v)=f0(x)$ma{x}_{\lambda ,v}L(x,\lambda ,v)=f_0(x)$
• 当x不在可行域，在定义域D内时，如果hi(x)≠0$h_i(x)\ne 0$ ，可以令对应的vi=∞$v_i=\mathrm{\infty }$ ,从而maxλ,vL(x,λ,v)=∞$ma{x}_{\lambda ,v}L(x,\lambda ,v)=\mathrm{\infty }$ ，即p∗=∞$p^{\ast }=\mathrm{\infty }$ ，该问题不可行。如果fi(x)≥0$f_i(x)\ge 0$ ,也可以令对应的λi=∞${\lambda }_i=\mathrm{\infty }$ ，从而maxλ,vL(x,λ,v)=∞$ma{x}_{\lambda ,v}L(x,\lambda ,v)=\mathrm{\infty }$ ，即p∗=∞$p^{\ast }=\mathrm{\infty }$ ，该问题不可行。

也就是，x在可行域时，主问题与原约束问题等价。当x不在可行域时，主问题返回p∗=∞$p^{\ast }=\mathrm{\infty }$ ，原问题不可行。综上，主问题与原问题等价。

对偶函数

定义对偶函数为：

g(λ,v)=minx∈D(L(x,λ,v))=minx∈D(f0(x)+f(x)Tλ+h(x)Tv)$g(\lambda ,v)=mi{n}_{x\in D}(L(x,\lambda ,v))=mi{n}_{x\in D}(f_0(x)+f(x{)}^T\lambda +h(x{)}^{T}v)$

括号里的函数θ(λ,v)=(f0(x)+f(x)Tλ+h(x)Tv)$\theta (\lambda ,v)=(f_0(x)+f(x{)}^T\lambda +h(x{)}^{T}v)$ 可以看作是λ,v$\lambda ,v$ 的仿射函数（aTx+b$a^{T}x+b$） ，仿射函数是既凸且凹的。这里不妨认为是凹函数。根据凸函数的逐点最大性质，可以得到凹函数的逐点最小函数是凹函数。g(λ,v)$g(\lambda ,v)$ 是θ(λ,v)$\theta (\lambda ,v)$ 函数的逐点下确界，因此g(λ,v)$g(\lambda ,v)$ 是凹函数 （与原函数的凹凸性质无关）。

注意，这里的x是属于定义域的。

对偶函数提供了最优值的下界，证明如下：

如果x~$\tilde{x}$ 是一个可行点，则

因此，当x~$\tilde{x}$ 取最优解时， g(λ,v)≤f0(x∗)=p∗$g(\lambda ,v)\le f_0(x^{\ast })=p^{\ast }$

对偶问题

定义对偶问题为：

目标函数为 maxλ≥0,vminx∈D(L(x,λ,v))$ma{x}_{\lambda \ge 0,v}mi{n}_{x\in D}(L(x,\lambda ,v))$

这是一个凹函数在凸集（λ≥0$\lambda \ge 0$）上的最大化问题，也就是凸函数在凸集上的最小化问题。这是一个凸优化问题，其最优解记为d∗$d^{\ast }$ ，对应的极值点为λ∗,v∗${\lambda }^{\ast },v^{\ast }$ 。

其特点是：不论原问题是否为凸优化问题，其对偶问题为凸优化问题，且有d∗≤p∗$d^{\ast }\le p^{\ast }$

强弱对偶解释

弱对偶：d∗≤p∗$d^{\ast }\le p^{\ast }$ ,不论原问题是否为凸优化问题，

强对偶：d∗=p∗$d^{\ast }=p^{\ast }$ ，通常是不成立的。当时对于凸优化问题，当满足一定条件之后就会成立，这些条件称为限定条件。其中一个比较简单的限定条件是Slater条件。

对于凸优化问题，如果满足Slater条件（对于不等式约束，存在内点x，使得fi(x)<0,i=1,...,m$f_i(x)<0,i=1,...,m$ 均成立，且hi(x)=0$h_i(x)=0$）则对偶问题为强对偶。（这是一个充分条件）

注意，在Slater条件中，如果fi(x),i=1,...k$f_i(x),i=1,...k$ 是仿射函数，则Slater条件简化为：

fi(x)≤0,i=1,...k,fi(x)<0,i=k+1,...,m,hi(x)=0$f_i(x)\le 0,i=1,...k,f_i(x)<0,i=k+1,...,m,h_i(x)=0$

从工程角度，凸优化问题通常满足强对偶。

从对偶问题求解主问题

假设fi(x),hi(x)$f_i(x),h_i(x)$ 可微，有KKT条件：

1. fi(x∗)≤0,i=1,...,m$f_i(x^{\ast })\le 0,i=1,...,m$ 即∇λL(x∗,λ,v)=0${\mathrm{\nabla }}_{\lambda }L(x^{\ast },\lambda ,v)=0$
2. hi(x∗)=0,i=1,...,p;即∇vL(x∗,λ,v)=0$h_i(x^{\ast })=0,i=1,...,p;即{\mathrm{\nabla }}_{v}L(x^{\ast },\lambda ,v)=0$
3. λi≥0${\lambda }_i\ge 0$ 拉格朗日函数不等式条件
4. λ∗ifi(x∗)=0${\lambda }_i^{\ast }{f}_i(x^{\ast })=0$ 互补条件，λ∗i,fi(x∗)${\lambda }_i^{\ast },f_i(x^{\ast })$ 不同时为零，可以用于筛选解。
5. ∇xL(x∗,λ∗,v∗)=0${\mathrm{\nabla }}_{x}L(x^{\ast },{\lambda }^{\ast },v^{\ast })=0$ 即∇f0(x∗)+∑mi=1λ∗i∇fi(x∗)+∑pi=1v∗i∇hi(x∗)=0$\mathrm{\nabla }{f}_0(x^{\ast })+\sum _{i=1}^m{\lambda }_i^{\ast }\mathrm{\nabla }{f}_i(x^{\ast })+\sum _{i=1}^p{v}_i^{\ast }\mathrm{\nabla }{h}_i(x^{\ast })=0$

其中，1,2为主问题可行性条件，3为对偶问题可行性条件，4为互补条件，5为stationarity条件。

互补条件为什么不同时为零？

必要性

假设强对偶成立（例如满足Slater条件），(x∗,λ∗,v∗)$(x^{\ast },{\lambda }^{\ast },v^{\ast })$ 是主问题和对偶问题的解，则可以推导得到：

因此，上面的不等式中等号成立，可以得到：

• λ∗ifi(x∗)=0${\lambda }_i^{\ast }{f}_i(x^{\ast })=0$ 这个称为互补条件
• g(λ∗,v∗)=L(x∗,λ∗,v∗)$g({\lambda }^{\ast },v^{\ast })=L(x^{\ast },{\lambda }^{\ast },v^{\ast })$ 即L(x,λ∗,v∗)$L(x,{\lambda }^{\ast },v^{\ast })$ 在x∗$x^{\ast }$ 处取得极值，因此，∇xL(x∗,λ∗,v∗)=0${\mathrm{\nabla }}_{x}L(x^{\ast },{\lambda }^{\ast },v^{\ast })=0$

因此：如果(x∗,λ∗,v∗)$(x^{\ast },{\lambda }^{\ast },v^{\ast })$ 是主问题和对偶问题的解，且满足强对偶，则(x∗,λ∗,v∗)$(x^{\ast },{\lambda }^{\ast },v^{\ast })$ 满足KKT条件。

注意，这里并没有限定原问题是凸问题

充分性

如果 (x∗,λ∗,v∗)$(x^{\ast },{\lambda }^{\ast },v^{\ast })$满足KKT条件，则 ：

g(λ∗,v∗)=(f0(x∗)+f(x∗)Tλ∗+h(x∗)Tv∗)=f0(x∗)$g({\lambda }^{\ast },v^{\ast })=(f_0(x^{\ast })+f(x^{\ast }{)}^T{\lambda }^{\ast }+h(x^{\ast }{)}^T{v}^{\ast })=f_0(x^{\ast })$

第一个等号成立是由于stationarity 条件，第二个等号成立是互补条件。

因此，如果 (x∗,λ∗,v∗)$(x^{\ast },{\lambda }^{\ast },v^{\ast })$满足KKT条件，则 (x∗,λ∗,v∗)$(x^{\ast },{\lambda }^{\ast },v^{\ast })$分别是主问题和对偶问题的解。

结论

KKT总是充分条件，当满足强对偶时，是必要条件。

以上称为一阶KKT条件，类比于无约束问题中的梯度等于0（当没有约束时，KKT的第5个条件约减为∇f0(x∗)=0$\mathrm{\nabla }{f}_0(x^{\ast })=0$）。因此，对于凸优化问题，满足一阶KKT条件就满足强对偶，可以通过求解一阶KKT条件得到问题的解。（类比于无约束问题的直接法（梯度为0法））。

对于非凸问题，一阶KKT条件是局部极小解的必要条件，还需要结合二阶KKT条件进行判断。（类比与无约束问题中的梯度=0，可能是极小、极大或鞍点，需要结合Hessian矩阵进行判断）。

总结主对问题

案例

案例1 最小二范数解

该问题是一个凸优化问题，并且满足强对偶，首先写出其拉格朗日形式及对偶函数。为了求出对偶函数的形式，将拉格朗日函数对x求偏导，得到x∗$x^{\ast }$ 关于v的函数。带入得到对偶函数g(v)$g(v)$ 的形式。

原问题转换为对偶问题，再次求得，得到v∗,d∗$v^{\ast },d^{\ast }$ ，并进一步得到x∗$x^{\ast }$ 。

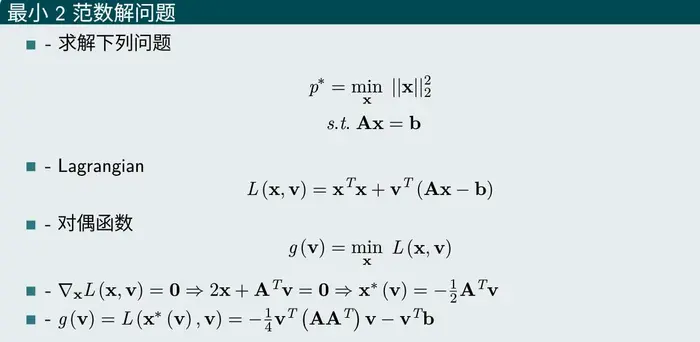
案例2 LP问题

LP问题是典型凸优化问题，写出拉格朗日形式及对偶函数。

观察对偶函数，后一项是关于x的线性变化，类似于一条直线，因此，当系数为0时，会取得0，否则会取得−∞$-\mathrm{\infty }$ ，因此，对偶函数可以写成如下形式。从而对偶问题也是LP问题。

因此，LP问题的对偶问题也是LP问题。可以采用内点法求解。（具体可以参考Boyd书中的第11章）

4.5 SVM

SVM主要用于求解分类问题，通过扩展也可以求解回归问题（SVR）

SVM建模

对于分类问题(假定线性可分)，其目标是求一个超平面wTx+b$w^{T}x+b$ 将空间划分为两个半空间，分别对应正样本和负样本。这种超平面可能有很多种，要寻找最优的超平面。最优解要具有鲁棒性，能够尽可能的分开这两类样本。

为了数学描述，定义几何间隔（Geometric margin）：所有样本点中，距离超平面最近的样本点到超平面的距离。（点到超平面的距离(参见)[1.2.2 超平面]）

M=mini(|wTxi+b|∥w∥2)$M=mi{n}_i({\displaystyle \frac{|w^T{x}_i+b|}{\Vert w{\Vert }_2}})$

因此，SVM的目标函数可以写为：

maxw,b{mini(|wTxi+b|∥w∥2)}$ma{x}_{w,b}\{mi{n}_i({\displaystyle \frac{|w^T{x}_i+b|}{\Vert w{\Vert }_2}})\}$

下面对目标函数进行化简，首先，|wTxi+b|=yi(wTxi+b)$|w^T{x}_i+b|=y_i(w^T{x}_i+b)$ ，这里yi$y_i$ 是样本标签，正样本定义为+1，负样本定义为-1。此时目标函数写为：

maxw,b{1∥w∥2mini(yi(wTxi+b))}$ma{x}_{w,b}\{{\displaystyle \frac{1}{\Vert w{\Vert }_2}}mi{n}_i(y_i(w^T{x}_i+b))\}$

如果将w，b同时缩放k倍，点到超平面的距离（H(y)=|wTy+b|∥w∥$H(y)={\displaystyle \frac{|w^{T}y+b|}{\Vert w\Vert }}$）是不变的。因此，可以通过缩放，使得对于距离超平面最近的点有：yi(wTxi+b)=1$y_i(w^T{x}_i+b)=1$

则，yi(wTxi+b)≥1$y_i(w^T{x}_i+b)\ge 1$ 成立。

此时，目标函数可以写为：

maxw,b{1∥w∥2},subject toyi(wTxi+b)≥1$ma{x}_{w,b}\{{\displaystyle \frac{1}{\Vert w{\Vert }_2}}\},subjectto{y}_i(w^T{x}_i+b)\ge 1$

进一步可以写为：1/2是为了求导方便

minw,b{12∥w∥22},subject toyi(wTxi+b)≥1$mi{n}_{w,b}\{{\displaystyle \frac{1}{2}}\Vert w{\Vert }_2^2\},subjectto{y}_i(w^T{x}_i+b)\ge 1$

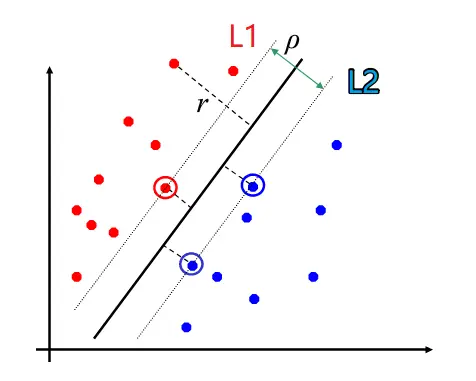
其几何解释为：下图中L1:wTx+b=1$L1:w^{T}x+b=1$, L2:wTx+b=−1$L2:w^{T}x+b=-1$ ，其中红色和蓝色距离超平面最近点的距离都是1∥w∥2${\displaystyle \frac{1}{\Vert w{\Vert }_2}}$ ,因此ρ=2∥w∥2$\rho ={\displaystyle \frac{2}{\Vert w{\Vert }_2}}$ 。SVM的目标就是使得ρ$\rho$ 最大，最近点到超平面的向量称为支撑向量。

SVM求解

解法一

通过对比4.3节凸优化问题实例中的例子，SVM问题可以转换成标准QP问题。可以直接使用内点法进行求解。但是，当样本数量N很大时，这种方法效率较低。

解法二，SVM对偶问题

首先写出SVM问题的拉格朗日函数：

L(w,b,λ)=12wTw+∑Ni=1λi(1−yi(wTxi+b)$L(w,b,\lambda )={\displaystyle \frac{1}{2}}{w}^{T}w+\sum _{i=1}^N{\lambda }_i(1-y_i(w^T{x}_i+b)$

因此，其对偶问题的最优解为：

d∗=maxλ≥0{minw,bL(w,b,λ)}$d^{\ast }=ma{x}_{\lambda \ge 0}\{mi{n}_{w,b}L(w,b,\lambda )\}$

其中，对偶函数minw,bL(w,b,λ)$mi{n}_{w,b}L(w,b,\lambda )$ 可以通过拉格朗日函数分别对w和b求偏导等于0得到，即

∇wL(w,b,λ)=w−∑Ni=1λiyixi=0→w=∑Ni=1λiyixi${\mathrm{\nabla }}_{w}L(w,b,\lambda )=w-\sum _{i=1}^N{\lambda }_i{y}_i{x}_i=0\to w=\sum _{i=1}^N{\lambda }_i{y}_i{x}_i$

∇bL(w,b,λ)=∑Ni=1λiyi=0${\mathrm{\nabla }}_{b}L(w,b,\lambda )=\sum _{i=1}^N{\lambda }_i{y}_i=0$

将上式得到的w，b带入拉格朗日函数，则对偶问题变为：

可以看到，上面的问题是关于λ$\lambda$ 的QP问题。QP问题的对偶问题也是QP问题 从这个角度，转换为对偶问题并没有简化SVM的计算量，但是这个问题有一个快速SMO算法。

假定对偶问题能够求解出λ∗${\lambda }^{\ast }$ ,由于SVM问题目标函数为凸函数，且满足Slater条件，因此是强对偶问题。满足KKT条件，则：

从互补条件可以看出：

• λ∗i>0,yi(w∗Txi+b∗)=1${\lambda }_i^{\ast }>0,y_i({w^{\ast }}^T{x}_i+b^{\ast })=1$ ，对应支撑向量，对w∗$w^{\ast }$ 有贡献
• λ∗i=0,yi(w∗Txi+b∗)>1${\lambda }_i^{\ast }=0,y_i({w^{\ast }}^T{x}_i+b^{\ast })>1$ ，对应非支撑向量，对w∗$w^{\ast }$ 无贡献，但是对求解λ∗${\lambda }^{\ast }$ 有贡献。

因此，λi=0${\lambda }_i=0$ 对应的点在最后求w$w$ 时可以不保存。剩余点满足yj(w∗Txj+b∗)=1$y_j({w^{\ast }}^T{x}_j+b^{\ast })=1$ ,将w∗$w^{\ast }$ 带入可以求得b∗=yj−∑Ni=1λ∗iyixTixj$b^{\ast }=y_j-\sum _{i=1}^N{\lambda }_i^{\ast }{y}_i{x}_i^T{x}_j$

最终，SVM的决策函数为：

SMO算法

对于以下无约束问题

maxλW(λi,i=1,...m)$ma{x}_{\lambda }W({\lambda }_i,i=1,...m)$

可以通过依次固定除λi${\lambda }_i$ 之外的其他值，来求解λi${\lambda }_i$ 的方式迭代求解，只要保证每次迭代函数值是上升的。

将这种方法应用到SVM中，但是由于约束条件∑λiyi=0$\sum {\lambda }_i{y}_i=0$ ，因此每次保留两个参数λi,λj${\lambda }_i,{\lambda }_j$自由，固定其他参数，求解SVM对偶问题，求得λi,λj${\lambda }_i,{\lambda }_j$ ，其中，由于有约束条件，λj${\lambda }_j$ 可以由λi${\lambda }_i$ 来表示。因此，每次是求解关于λi${\lambda }_i$ 的单变量QP问题，仅有的约束是λi≥0${\lambda }_i\ge 0$ ，是一个一维搜索问题。

参考文献：Platt. J, Sequential minimal optimization: A fast algorithm for training support vector machines. Technical Report MSR-TR-98-14, Microsoft Research.

SVM扩展

软间隔

在建立SVM模型时，假定正负样本是线性可分的。但是，实际有些时候，样本不是完全线性可分的，会出现交错的情况，例如下图。

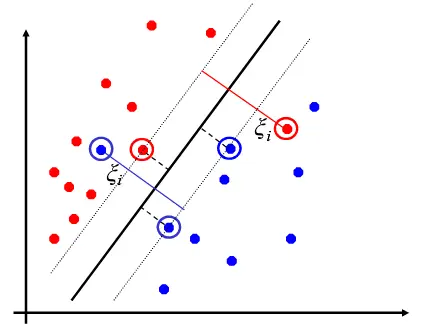
这时，如果采用以下模型

minw,b{12∥w∥22},subject toyi(wTxi+b)≥1$$\begin{gathered} mi{n}_{w,b}\{{\displaystyle \frac{1}{2}}\Vert w{\Vert }_2^2\}, \\ subjectto{y}_i(w^T{x}_i+b)\ge 1 \end{gathered}$$

可能就没有可行解。针对这种情况，建立如下模型，称为软间隔

minw,b{12∥w∥22+C∑Ni=1ξi},subject toyi(wTxi+b)≥1−ξi;i=1,...,Nξi≥0$$\begin{gathered} mi{n}_{w,b}\{{\displaystyle \frac{1}{2}}\Vert w{\Vert }_2^2+C\sum _{i=1}^N{\xi }_i\}, \\ subjectto{y}_i(w^T{x}_i+b)\ge 1-{\xi }_i;i=1,...,N \\ {\xi }_i\ge 0 \end{gathered}$$

这个就是4.3中给出的例子，也是一个QP问题。其中，ξi${\xi }_i$ 为容忍度，可以优化得到。C为参数，需要根据经验调整。

这个问题跟几何间隔的问题一样，可以转换为对偶问题，然后通过SMO算法求解。

核函数

当样本完全线性不可分时，例如下图中左图所示，其中一个方法是使用非线性拟合，另一个方法是通过特征映射x↦ϕ(x)$x\mapsto \varphi (x)$ ,将低维特征映射到高维空间，在这个高维空间中，可能就线性可分，如图中右图所示。

这样，经过映射后，原SVM模型中的x由ϕ(x)$\varphi (x)$ 代替：

minw,b{12∥w∥22},subject toyi(wTϕ(xi)+b)≥1$$\begin{gathered} mi{n}_{w,b}\{{\displaystyle \frac{1}{2}}\Vert w{\Vert }_2^2\}, \\ subjectto{y}_i(w^T\varphi (x_i)+b)\ge 1 \end{gathered}$$

则对偶问题转换为：

其中，直接计算ϕ(xi)Tϕ(xj)$\varphi (x_i{)}^T\varphi (x_j)$ 是很困难的，一是由于维度大，二是由于ϕ(x)$\varphi (x)$ 的形式难以确定。

因此，这里定义核函数：

κ(xi,xj)=ϕ(xi)Tϕ(xj)$\kappa (x_i,x_j)=\varphi (x_i{)}^T\varphi (x_j)$

则最终决策函数可以写为：

常见核函数有

在实际使用过程中，一般先用高斯核试一下效果。

更详细的相关模型可以参照“Pattern Recognition and Machine Learning”一书