凸优化问题
先转载几个链接,关于理论的介绍。
作者:王业磊
链接:https://www.zhihu.com/question/20343349/answer/17347657
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
数学中最优化问题的一般表述是求取 ,使
,使 ,其中
,其中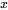 是n维向量,
是n维向量, 是
是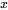 的可行域,
的可行域, 是
是 上的实值函数。
上的实值函数。
凸优化问题是指 是闭合的凸集且
是闭合的凸集且 是
是 上的凸函数的最优化问题,这两个条件任一不满足则该问题即为非凸的最优化问题。
上的凸函数的最优化问题,这两个条件任一不满足则该问题即为非凸的最优化问题。
其中, 是 凸集是指对集合中的任意两点
是 凸集是指对集合中的任意两点 ,有
,有 ,即任意两点的连线段都在集合内,直观上就是集合不会像下图那样有“凹下去”的部分。至于闭合的凸集,则涉及到闭集的定义,而闭集的定义又基于开集,比较抽象,不赘述,这里可以简单地认为闭合的凸集是指包含有所有边界点的凸集。
,即任意两点的连线段都在集合内,直观上就是集合不会像下图那样有“凹下去”的部分。至于闭合的凸集,则涉及到闭集的定义,而闭集的定义又基于开集,比较抽象,不赘述,这里可以简单地认为闭合的凸集是指包含有所有边界点的凸集。

 是凸函数是指对于定义域
是凸函数是指对于定义域 中任意两点
中任意两点 ,有
,有 (这里应该是小于等于号,作者注),直观上就是
(这里应该是小于等于号,作者注),直观上就是 向下凸出,如下图示意。
向下凸出,如下图示意。
<img src="https://pic1.zhimg.com/50/3a05acd2b63840bd7f79333c647411f0_hd.jpg" data-rawwidth="300" data-rawheight="156" class="content_image" width="300">
实际建模中判断一个最优化问题是不是凸优化问题一般看以下几点:
凸优化问题是指
其中,
<img src="https://pic1.zhimg.com/50/3a05acd2b63840bd7f79333c647411f0_hd.jpg" data-rawwidth="300" data-rawheight="156" class="content_image" width="300">
实际建模中判断一个最优化问题是不是凸优化问题一般看以下几点:
- 目标函数
如果不是凸函数,则不是凸优化问题
- 决策变量
中包含离散变量(0-1变量或整数变量),则不是凸优化问题
- 约束条件写成
时,
如果不是凸函数,则不是凸优化问题
资料来自维基,稍有删减改动。
以上重要部分都已经标出,关键就是1)定义域是闭合的凸集 2)函数满足凸函数定义。
其实在自己理解问题和听课时,直观理解更好。
比如吴恩达教授提到的1/2*(y'-y)^2这个函数,课件中提到他是一个非凸函数。那么画下图来是底下这样的。
可以看到这是个马鞍形的,并没有满足(下)凸函数条件,有可能出现两点连线的中值小于函数在该中间点的取值的情况。或者二维看不出来的话就转为一维度来看,切一条线初来,明显是上凸的,这种函数存在的最大问题,知乎回答也提及了,就是局部最优解有可能不是全局最优解。根据这种函数定义出来的损失函数(或者叫优化函数)会容易陷入局部最优解的问题,所以一般不采用这种函数。
底下这个函数就很棒了。
PS,记住底下这个公式,excel画曲面图必备。
=$A2^2/2+B$1^2/2-2*$A2*B$1
