【机器学习】求解逻辑回归参数（梯度上升算法和牛顿法）

这篇博客【链接】我们简单介绍了逻辑回归模型，留下了一个问题：怎么求解使 $J (θ)$ 最大的 $θ$ 值呢？

J (θ) = \sum_{i = 1}^{m} (y^{(i)} l o g h_{θ} (x^{(i)}) + (1 - y^{(i)}) l o g (1 - h_{θ} (x^{(i)})))

前面我们提到了用梯度上升法和牛顿法。那么什么是梯度上升法和牛顿法呢？

由于 $J (θ)$ 过于复杂，我们从一个简单的函数求极大值说起。
一元二次函数

f (x) = - x^{2} + 4 x

图像如下：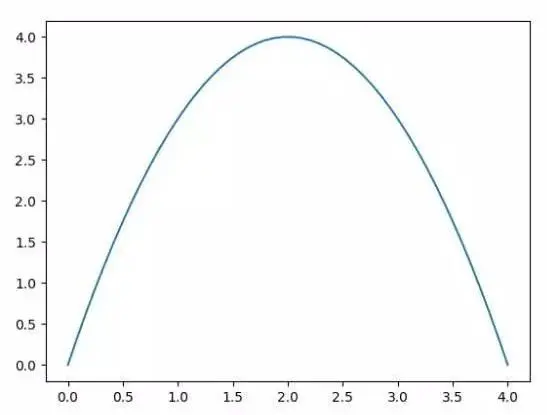

根据高中所学知识:
1. 求极值，先求函数的导数

f^{'} (x) = - 2 x + 4

2. 令导数为0，可求出

x = 2

即取得函数

f (x)

的极大值。极大值等于

f (2) = 4

但是真实环境中的函数不会像上面这么简单，就算求出了函数的导数，也很难精确计算出函数的极值。此时我们就可以用迭代的方法来做。就像爬坡一样，一点一点逼近极值。这种寻找最佳拟合参数的方法，就是最优化算法。爬坡这个动作用数学公式表达即为：

x_{i + 1} = x_{i} + α \frac{\partial f (x_{i})}{\partial x_{i}}

其中，

α

为步长，也就是学习速率，控制更新的幅度。效果如下图：
【机器学习】求解逻辑回归参数（梯度上升算法和牛顿法）

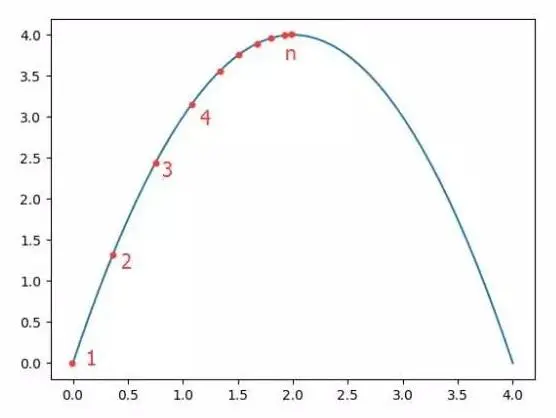
比如从(0,0)开始，迭代路径就是1->2->3->4->…->n，直到求出的x为函数极大值的近似值，停止迭代。
这一过程，就是梯度上升算法。那么同理， $J (θ)$ 这个函数的极值，也可以这么求解。公式可以写为：

θ_{j} := θ_{j} + α \frac{\partial J (θ)}{\partial θ_{j}}

那么，我们现在只要求出 $J (θ)$ 的偏导，就可以利用梯度上升算法求解 $J (θ)$ 的极大值了。

J (θ) = \sum_{i = 1}^{m} {y^{(i)} l o g h_{θ} (x^{(i)}) + (1 - y^{(i)}) l o g (1 - h_{θ} (x^{(i)}))}

h_{θ} (x) = g (θ^{T} x) = \frac{1}{1 + e^{- θ^{T} x}}

令：

g (z) = \frac{1}{1 + e^{- z}}

求导：

g^{'} (z) = \frac{e^{- z}}{(1 + e^{- z})^{2}} = \frac{1}{1 + e^{- z}} * \frac{e^{- z}}{1 + e^{- z}} = \frac{1}{1 + e^{- z}} * (1 - \frac{1}{1 + e^{- z}}) = g (z) * (1 - g (z))

可得：

g^{'} (θ^{T} x) = g (θ^{T} x) * (1 - g (θ^{T} x))

求 $J (θ) 的偏导$

\frac{\partial J (θ)}{\partial θ_{j}} = \sum_{i = 1}^{m} (\frac{y^{(i)}}{h_{θ} (x^{(i)})} - \frac{1 - y^{(i)}}{1 - h_{θ} (x^{(i)})}) * \frac{\partial h_{θ} (x^{(i)})}{\partial θ_{j}}

= \sum_{i = 1}^{m} (\frac{y^{(i)}}{g (θ^{T} x^{(i)})} - \frac{1 - y^{(i)}}{1 - g (θ^{T} x^{(i)})}) * \frac{\partial g (θ^{T} x^{(i)})}{\partial θ_{j}}

= \sum_{i = 1}^{m} (\frac{y^{(i)}}{g (θ^{T} x^{(i)})} - \frac{1 - y^{(i)}}{1 - g (θ^{T} x^{(i)})}) * g (θ^{T} x^{(i)}) * (1 - g (θ^{T} x^{(i)})) * \frac{\partial θ^{T} x^{(i)}}{\partial θ_{j}}

其中：

\frac{\partial θ^{T} x^{(i)}}{\partial θ_{j}} = \frac{\partial (θ_{1} x_{1}^{(i)} + θ_{2} x_{2}^{(i)} + θ_{3} x_{3}^{(i)} + . . . + θ_{n} x_{n}^{(i)})}{\partial θ_{j}} = x_{j}^{(i)}

上 式 = \sum_{i = 1}^{m} {y^{(i)} (1 - g (θ^{T} x^{(i)})) - (1 - y^{(i)}) (g (θ^{T} x^{(i)})} * x_{j}^{(i)} = \sum_{i = 1}^{m} (y^{(i)} - g (θ^{T} x^{(i)})) * x_{j}^{(i)}

综上：

θ_{j} := θ_{j} + α \sum_{i = 1}^{m} (y^{(i)} - h_{θ} (x^{(i)})) * x_{j}^{(i)}

θ_{j} := θ_{j} + α (y^{(i)} - h_{θ} (x^{(i)})) * x_{j}^{(i)}

同样，我们先来看个简单的例子。求函数值为0时的x的值。
用牛顿法迭代公式：

x_{n + 1} = x_{n} - \frac{f (x_{n})}{f^{'} (x_{n})} x_{n + 2} = x_{n + 1} - \frac{f (x_{n + 1})}{f^{'} (x_{n + 1})}

【机器学习】求解逻辑回归参数（梯度上升算法和牛顿法）

这个迭代公式的意思就是：在 $x = x_{1}$ 时，求得 $(x_{1}, f (x_{1}))$ 的切线与x轴的交点为 $x_{2}$ ，再求 $(x_{2}, f (x_{2}))$ 的切线与x轴的交点 $x_{3}$ ，依次迭代，直到找到满足要求的点。

然而，对于 $J (θ)$ 我们需要求得一阶导数为0的点，那么牛顿法迭代公式可以更新为：

x_{n + 1} = x_{n} - \frac{J^{'} (x_{n})}{J^{″} (x_{n})} x_{n + 2} = x_{n + 1} - \frac{J^{'} (x_{n + 1})}{J^{″} (x_{n + 1})}

在多元的情况下， $J^{″} (x_{n}) = H_{ℓ (\hat{θ})}$ 海塞矩阵

H_{ℓ (\hat{θ})} = [\begin{matrix} \begin{aligned} \frac{\partial^{2} J}{\partial θ_{1} \partial θ_{1}} & \frac{\partial^{2} J}{\partial θ_{1} \partial θ_{2}} \\ \frac{\partial^{2} J}{\partial θ_{2} \partial θ_{1}} & \frac{\partial^{2} J}{\partial θ_{2} \partial θ_{2}} \end{aligned} \end{matrix}]

三阶海塞矩阵形式为：

H_{ℓ (\hat{θ})} = [\begin{matrix} \begin{aligned} \frac{\partial^{2} J}{\partial θ_{1} \partial θ_{1}} & \frac{\partial^{2} J}{\partial θ_{1} \partial θ_{2}} & \frac{\partial^{2} J}{\partial θ_{1} \partial θ_{3}} \\ \frac{\partial^{2} J}{\partial θ_{2} \partial θ_{1}} & \frac{\partial^{2} J}{\partial θ_{2} \partial θ_{2}} & \frac{\partial^{2} J}{\partial θ_{2} \partial θ_{3}} \\ \frac{\partial^{2} J}{\partial θ_{3} \partial θ_{1}} & \frac{\partial^{2} J}{\partial θ_{3} \partial θ_{2}} & \frac{\partial^{2} J}{\partial θ_{3} \partial θ_{3}} \end{aligned} \end{matrix}]

H_{ℓ (\hat{θ})} = [\begin{matrix} \begin{aligned} \sum_{i = 1}^{n} h_{θ} (x_{i}) (1 - h_{θ} (x_{i})) x_{i, 1} x_{i, 1}, & \sum_{i = 1}^{n} h_{θ} (x_{i}) (1 - h_{θ} (x_{i})) x_{i, 1} x_{i, 2}, & \sum_{i = 1}^{n} h_{θ} (x_{i}) (1 - h_{θ} (x_{i})) x_{i, 1} \\ \sum_{i = 1}^{n} h_{θ} (x_{i}) (1 - h_{θ} (x_{i})) x_{i, 2} x_{i, 1}, & \sum_{i = 1}^{n} h_{θ} (x_{i}) (1 - h_{θ} (x_{i})) x_{i, 2} x_{i, 2}, & \sum_{i = 1}^{n} h_{θ} (x_{i}) (1 - h_{θ} (x_{i})) x_{i, 2}, \\ \sum_{i = 1}^{n} h_{θ} (x_{i}) (1 - h_{θ} (x_{i})) x_{i, 1}, & \sum_{i = 1}^{n} h_{θ} (x_{i}) (1 - h_{θ} (x_{i})) x_{i, 2}, & \sum_{i = 1}^{n} h_{θ} (x_{i}) (1 - h_{θ} (x_{i})) \end{aligned} \end{matrix}] h_{θ} (x_{i}) = \frac{1}{1 + e^{- z}} z = θ_{1} x_{i, 1} + θ_{2} x_{i, 2} + θ_{3}

一阶导数

\nabla J = - ⟨ \begin{matrix} \sum_{i = 1}^{n} (y_{i} - h_{θ} (x_{i})) x_{i, 1} \\ \sum_{i = 1}^{n} (y_{i} - h_{θ} (x_{i})) x_{i, 2} \\ \sum_{i = 1}^{n} (y_{i} - h_{θ} (x_{i})) \end{matrix} ⟩

注：
此外，还可以用sklearn自带函数求解逻辑回归参数
此三种方法的python3代码实现，点击这里，对比本文公式看。