PCA降维（Principal Component Analysis，主成分分析）

概述

$\quad$ 本文主要介绍一种一种降维方法，PCA（Principal Component Analysis，主成分分析）。在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。一般我们提到降维最容易想到的算法就是PCA。降维致力于解决三类问题：
$\quad$ 1）缓解数据维度灾难的问题；
$\quad$ 2）在压缩数据维度的同时让信息损失最小化；
$\quad$ 3）我们很难理解拥有几百个维度的数据，但是两三个维度的数据可以通过可视化来帮助我们理解数据。

一、数据的表示及降维问题

$\quad$ 在机器学习中，数据的表示一般采用向量的形式。假设我们的数据集
$T=\{x_1,x_2,...,x_n\}\in R^{n×n}$ 我们希望将这数据集 $T$ 降维至k维，即数据集 $T$ 变为
$T^{'}=\{x_1^{'},x_2^{'},...,x_k^{'}\}$ $\quad$ 我们希望数据集 $T^{'}$ 尽可能的代表原始数据集 $T$ 。我们知道在降维的过程中，肯定会导致数据的损失，但是我们如何才能做到让损失最小，且最能代表原始数据集呢？

二、向量的表示及基变换

$\quad$ 既然我们面对的数据被抽象为一组向量，那么下面我们有必要研究一些向量的数学性质，而这些数学性质将成为后续推导PCA的理论基础。
1、内积
$\quad$ 内积是两个向量的对应元素相乘，如下所示：
$(x_1,x_2,...,x_n)·(y_1,y_2,...,y_n)=x_1y_1+x_2y_2+...+x_ny_n$
2、基
$\quad$ 在线性代数中，有一个称呼叫做基向量，什么样的叫做基向量呢？假设在二维坐标系中，那么两个线性无关的向量，就可以称作是这个二维空间的基向量。我们还学过正交基，正交基就是两个线性无关且正交的向量，就可以称作这个二维空间的正交基。
PCA降维（Principal Component Analysis，主成分分析）
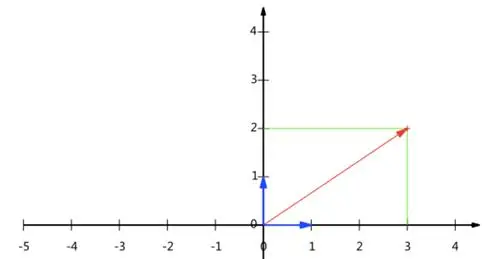
$\quad$ 如上所示，向量 $(3,2)$ 可以通过该坐标系中的两个正交基进行表示，这个正交基我们定义为： $(0,1)$ 和 $(1,0)$ ，那么 $(3,2)^T=3(1,0)^T+2(0,1)^T$
$\quad$ 我们再次假设基为： $(1,1)$ 和 $(-1,1)$ ，规范正交基是指两个正交向量的模为1，即上述的基通过除以模即可，即： $(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$ 和 $(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$
3、基变换的矩阵表示
$\quad$ 我们以 $(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$ 和 $(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$ 作为坐标系的基，那么我们如何将坐标 $(3,2)$ 转换到新基下呢？
$\quad$ 我们可以用矩阵的形式进行简洁的转化：
$\begin{pmatrix}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\-\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{pmatrix}$ $\begin{pmatrix}3\\2\end{pmatrix}$ = $\begin{pmatrix}\frac{5}{\sqrt{2}}\\-\frac{1}{\sqrt{2}}\end{pmatrix}$
$\quad$ 其中第一个矩阵的两行分别为两个基向量，再乘以原向量，就得到了该基下的新向量，即坐标。
$\quad$ 一般的，如果我们有M个N维向量，想将其变换为由R个N维向量表示的新空间中，那么首先将R个基按行组成矩阵A，然后将向量按列组成矩阵B，那么两矩阵的乘积AB就是变换结果，其中AB的第m列为A中第m列变换后的结果。即：
$\begin{bmatrix}p_1\\\vdots \\p_R\end{bmatrix}$ $\begin{bmatrix}a_1,\cdots,a_M\\\end{bmatrix}$ = $\begin{bmatrix}p_1a_1&\cdots&p_1a_M\\\vdots&\ddots&\vdots\\p_Ra_1&\cdots&p_Ra_M\end{bmatrix}$
$\quad$ 其中 $p_i$ 是一个行向量，表示第 $i$ 个基， $a_j$ 是一个列向量，表示第 $j$ 个原始数据记录。
$\quad$ 上述分析同时给矩阵相乘找到了一种物理解释：两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去。
4、方差
$\quad$ 一个字段的方差可以看作是每个元素与字段均值的差的平方和的均值，即：
$Var(a)=\frac{1}{m}\sum\limits_{i=1}^m(a_i-\mu)^2$
5、协方差
$Cov(x,y)=\frac{1}{m}\sum\limits_{i=1}^m(x_i-\overline{x})(y_i - \overline{y})$
$\quad$ 其中 $\overline x$ 和 $\overline y$ 分别表示两个随机变量所对应的观测样本的均值。
$\quad$ 当协方差为正时，说明x和y是正相关关系；协方差为负时，说明x和y是负相关关系；协方差为0时，说明x和y是相互独立的。

三、PCA的算法流程

下面我们来具体看下PCA的算法流程：
$\quad$ 输入： n维样本集 $T=(x_1,x_2,...,x_m)$ 要降到k维。
$\quad$ 输出： 降维后的样本集 $T^{'}$
$\quad$ 1）对所有样本进行中心化： $x_i=x_i-\frac{1}{m}\sum\limits_{j=1}^mx_j$
$\quad$ 2）计算样本的协方差矩阵 $XX^T$
$\quad$ 3）对矩阵 $XX^T$ 进行特征值分解
$\quad$ 4）取出最大的k个特征值对应的特征向量 $w_1,w_2,...,w_k$ ，将所有的特征向量标准化后，组成特征向量矩阵 $W$ 。
$\quad$ 5）对样本集中的每一个样本 $x_i$ ，转换为新的样本 $z_i=W^Tx_i$
$\quad$ 6）得到输出样本集 $T^{'}=(z_1,z_2,...,z_m)$

四、PCA例子

$\quad$ 下面举一个简单的例子，说明PCA的过程。
$\quad$ 假设我们的数据集有10个二维数 $(2.5,2.4), (0.5,0.7), (2.2,2.9), (1.9,2.2), (3.1,3.0)$ $, (2.3, 2.7), (2, 1.6), (1, 1.1), (1.5, 1.6), (1.1, 0.9)$ ，需要用PCA降到1维特征。
$\quad$ 首先我们对样本中心化，这里样本的均值为 $(1.81, 1.91)$ ,所有的样本减去这个均值向量后，即中心化后的数据集为 $(0.69, 0.49), (-1.31, -1.21), (0.39, 0.99), (0.09, 0.29)$ $, (1.29, 1.09), (0.49, 0.79), (0.19, -0.31), (-0.81, -0.81), (-0.31, -0.31)$ $, (-0.71, -1.01)$ 。
$\quad$ 现在我们开始求样本的协方差矩阵，由于我们是二维的，则协方差矩阵为：
$XX^T=\begin{pmatrix}cov(x_1,x_1)&cov(x_1,x_2)\\cov(x_2,x_1)&cov(x_2,x_2)\end{pmatrix}$ $\quad$ 对于我们的数据，求出协方差矩阵为：
$XX^T=\begin{pmatrix}0.616555556&0.615444444\\0.615444444&0.716555556\end{pmatrix}$ $\quad$ 求出特征值为 $(0.0490833989,1.28402771)$ ，对应的特征向量分别为：
$(0.735178656,0.677873399)^T$ $(-0.677873399,-0.735178656)^T$ $\quad$ 由于最大的k=1个特征值为1.28402771，对应的特征向量为: $(-0.677873399,-0.735178656)^T$ $\quad$ 则我们的 $W=(-0.677873399,-0.735178656)^T$ 。
$\quad$ 我们对所有的数据集 $z_i=W^Tx_i$ 进行投影，得到PCA降维后的10个一维数据集为：(-0.827970186， 1.77758033， -0.992197494， -0.274210416， -1.67580142， -0.912949103， 0.0991094375， 1.14457216, 0.438046137， 1.22382056)

PCA降维（Principal Component Analysis，主成分分析）

概述

一、数据的表示及降维问题

二、向量的表示及基变换

三、PCA的算法流程

四、PCA例子

相关推荐