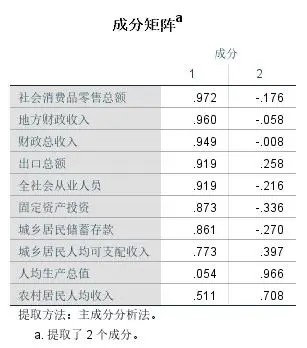
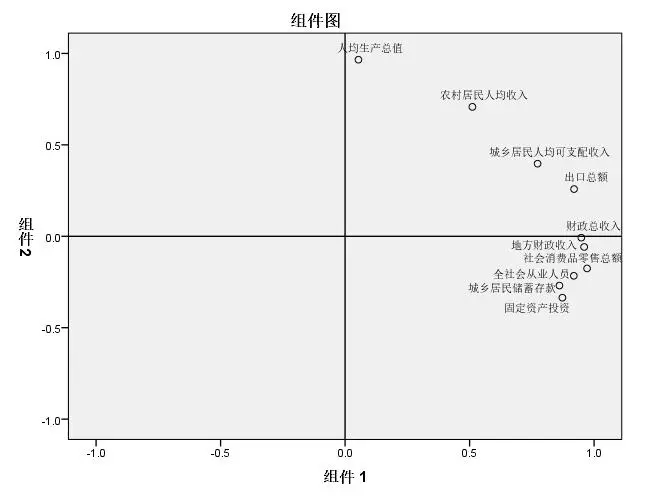
定义

主成分分析是利用降维的思想，在损失很少信息的前提下把多个指标转化为几个综合指标的多元统计方法。
转化生成的综合指标称之为主成分，其中每个主成分都是原始变量的线性组合，且各个主成分之间互不相关，这就使得主成分逼原始变量具有某些更优越的性能。

基本原理

如果用$x_1,x_2,...,x_p$x1​,x2​,...,xp​表示$p$p门课程，$c_1,c_2,...,c_p$c1​,c2​,...,cp​表示各门课程的权重，那么加权之和就是$s=c_1x_1+c_2x_2+...+c_px_p$s=c1​x1​+c2​x2​+...+cp​xp​我们希望选择适当的权重能更好的地区分学生的成绩。每个学生都对应这样一个综合成绩，即为$s_1,s_2,...s_n$s1​,s2​,...sn​，$n$n为学生人数。
◆我们需要的是能找到合适的$c_1,c_2,...,c_p$c1​,c2​,...,cp​，使得$s_1,s_2,...,s_n$s1​,s2​,...,sn​能尽可能的分散。
当然，必须加上某种限制，否则权值可选择无穷大而没有意义，通常规定
$c_1^2+c_2^2+...+c_p^2=1$c12​+c22​+...+cp2​=1
一个主成分不足以代表原来的$p$p个变量，因此需要寻找第二个乃至第三、四个主成分，第二个
主成分不应该再包含第一个主成分的信息，统计上的描述就是让这两个主成分的协方差为零，几何上就是这两个主成分的方向正交。具体确定各个主成分的方法如下。
设$Z_i$Zi​表示第$i$i个主成分，$i=1,2,...,p$i=1,2,...,p，可设
$\left\{\begin{array}{l} Z_{1}=c_{11} X_{1}+c_{12} X_{2}+\cdots+c_{1 p} X_{p} \\ Z_{2}=c_{21} X_{1}+c_{22} X_{2}+\cdots+c_{2 p} X_{p} \\ \cdots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots . . \\ Z_{p}=c_{p 1} X_{1}+c_{p 2} X_{2}+\cdots+c_{p p} X_{p} \end{array}\right.$⎩⎪⎪⎨⎪⎪⎧​Z1​=c11​X1​+c12​X2​+⋯+c1p​Xp​Z2​=c21​X1​+c22​X2​+⋯+c2p​Xp​⋯……………………..Zp​=cp1​X1​+cp2​X2​+⋯+cpp​Xp​​
其中对每一个$i$i，均有$c_1^2+c_2^2+...+c_p^2=1$c12​+c22​+...+cp2​=1

案例分析

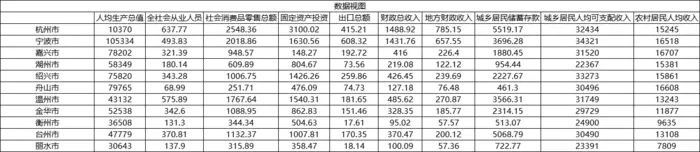
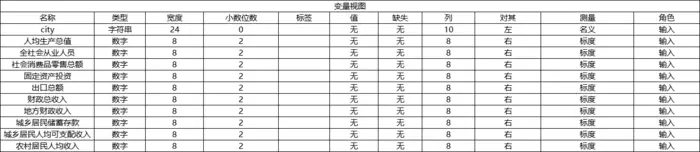
SPSS操作步骤
分析→降维→ 因子

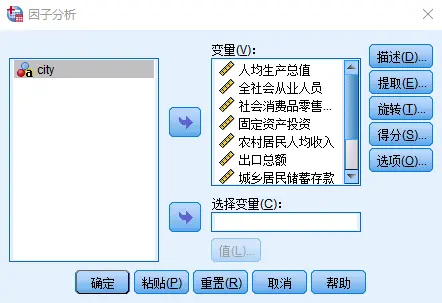
一般来说，由协方差矩阵出发求解主成分所得结果与由相关矩阵出发求解主成分所得结果有很大不同。对于度量单位不同的指标或取值范围彼此差异非常大的指标，不能直接由其协方差矩阵出发进行主成分分析，而应该考虑将数据标准化（从相关矩阵出发）。
对于同度量单位或取值范围在同量级的数据还是直接从协方差矩阵求解。

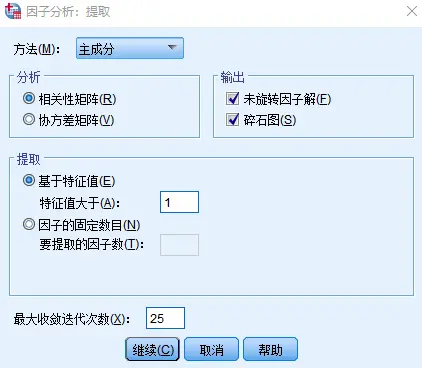
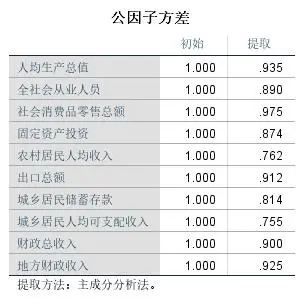
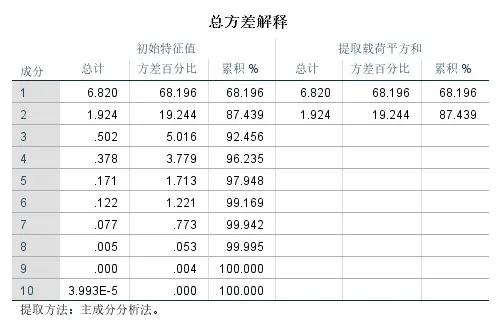
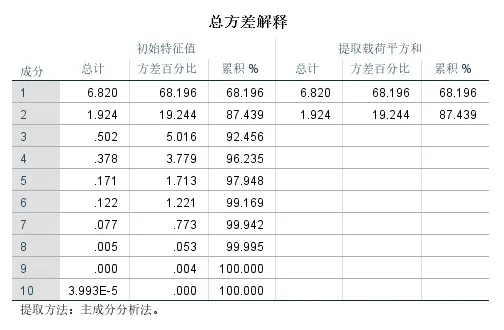
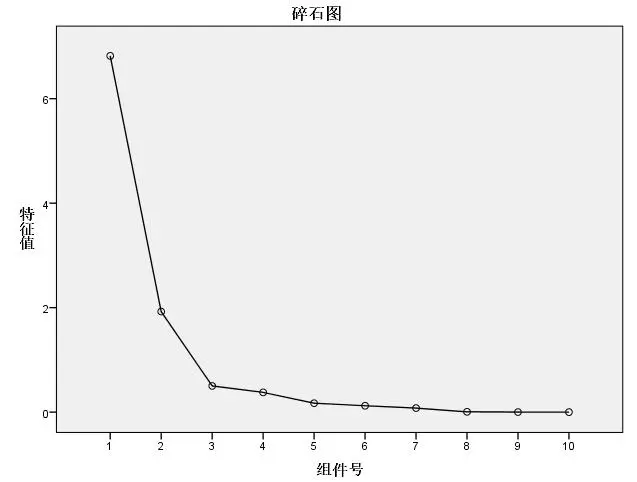
输出

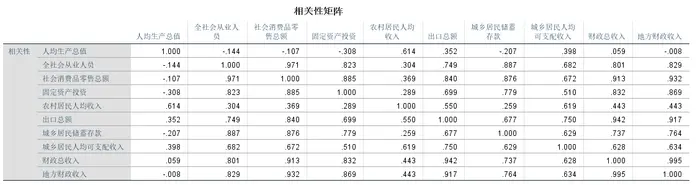
检验各因素之间有没有关联程度，一般情况下，$KMO$KMO值应大于等于$0.6$0.6，$Sig$Sig值应小于等于$0.05$0.05